|
Приднестровский государственный университет им. Т.Г. Шевченко |
|||||||||
|
Инженерно-технический институт |
|||||||||
|
Инженерно-технический факультет |
|||||||||
|
Кафедра программного обеспечения вычислительной техники и автоматизированных систем |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
КУРСОВАЯ РАБОТА |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
по дисциплине |
|||||||||
|
«Информатика и программирование» |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
тема: «ПРОГРАММНАЯ РЕАЛИЗАЦИЯ РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ» |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Работу выполнила |
|||
|
|
|
|
|
|
|
студентка группы ИТ13ДР62ИС1 |
|||
|
|
|
|
|
|
|
Арабаджи Федор Иванович |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Руководитель |
|||
|
|
|
|
|
|
|
ст. преподаватель |
|||
|
|
|
|
|
|
|
Белоконь О.С. |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тирасполь, 2014
|
|||||||||
ЗАДАНИЕ
на курсовую работу по дисциплине
«ПРОГРАММИРОВАНИЕ»
Студента группы ________ - ___________________
Тема: «____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________»
утверждена протоколом кафедры _________ № _____ от «____» ____________ 20___ г.
Цель курсовой работы:
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Задачи курсовой работы:
________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Результаты курсовой работы:
______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
___________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
График обязательных консультаций:
|
Дата консультации |
Подпись студента |
Подпись руководителя |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Дата сдачи записки на регистрацию «_____» __________20__ г.
Дата защиты курсовой работы «_____» __________20__ г.
Задание принял к исполнению «_____» __________20__ г. ___________/________________/
Руководитель работы ______________________ /________________/
СОДЕРЖАНИЕ
|
ВВЕДЕНИЕ……………………………………………………………………… |
4 |
|
1 ПОСТАНОВКА ЗАДАЧИ……………………………………………………. |
6 |
|
2 ОПИСАНИЕ ПРЕДМЕТНОЙ ОБЛАСТИ…………………………………... |
7 |
|
2.1 Метод Гаусса…………………………………………………………… |
7 |
|
2.2 Метод Крамера……………………………………………………......... |
9 |
|
2.3 Метод обратной матрицы……………………………………………... |
10 |
|
3 РУКОВОДСТВО ПРОГРАММИСТА……………………………………….. |
11 |
|
3.1 Введение и общие сведения…………………………………………… |
11 |
|
3.2 Структура программного продукта…………………………………... |
11 |
|
3.3 Описание типов данных…………………………………………….…. |
13 |
|
3.4 Описание исходных текстов программного продукта……………..... |
13 |
|
3.5 Аппаратная и программная часть……………………………………... |
18 |
|
3.6 Результаты тестирования и опытной эксплуатации…………………. |
18 |
|
4 РУКОВОДСТВО ПОЛЬЗОВАТЕЛЯ……………………………………….... |
22 |
|
4.1 Введение…………………...…………………………………………… |
22 |
|
4.2 Системные требования………………………………………………… |
22 |
|
4.3 Установка программного продукта……………………………….….. |
22 |
|
4.4 Запуск и работа с программным продуктом…………………….…… |
22 |
|
4.5 Удаление программного продукта……………………………………. |
24 |
|
ЗАКЛЮЧЕНИЕ…………………………………………………………………. |
26 |
|
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ……………………………. |
27 |
Введение
Последние десятилетия характеризуются бурным развитием вычислительной техники. Расширяются области применения вычислительных машин и совершенствуются методы их использования. Созданы универсальные языки программирования и разработаны мощные операционные системы.
Сейчас невозможно представить себе какую-либо область деятельности, обходящуюся без применения компьютерной техники.
Компьютеры используются при проведении различных инженерных расчётов, при решении экономических задач, в процессе управления производством, при получении оценок производственных ситуаций и во многих других случаях.
Решение систем линейных алгебраических уравнений является одной из основных задач линейной алгебры. Эта задача имеет важное прикладное значение при решении научных и технических проблем. Кроме того, является вспомогательной при реализации многих алгоритмов вычислительной математики, математической физики, обработки результатов экспериментальных исследований.
Алгебраическое уравнение называется линейным, если оно содержит переменные только в первой степени и не содержит произведений переменных.
Решение систем линейных алгебраических уравнений является одной из фундаментальных задач математики. В частности, она возникает при решении краевых задач для дифференциальных и интегральных уравнений, к которым сводятся реальные проблемы техники, физики, экономики, математики и др. Подобные программы довольно популярны, в особенности среди пользователей глобальной сети Интернет. Они могут быть широко применимы в среде образовательных учреждений. Например, преподавателю необходимо проверить десятки работ студентов в короткий срок или составить варианты контрольных работ, помочь студенту в решении систем линейных уравнений и в их объяснении, так как программа будет содержать краткую теоретическую справку.
Чтобы быстро справится с решением системы линейных уравнений, можно воспользоваться средствами вычислительной техники – написать программу на языке программирования.
Учитывая современные возможности, можно облегчить процесс решения систем линейных уравнений. Данную задачу можно выполнить программно для упрощения и автоматизации процесса решения систем линейных уравнений методом Гаусса, методом Крамера, а также методом обратной матрицы с помощью Windows-приложения, реализованного средствами языка высокого уровня С#.
Данный продукт найдёт своё применение в сфере образования. В частности, например, учащиеся с помощью данной программы смогут проверить правильность решения систем линейных уравнений.
1 постановка задачи
В данной курсовой работе необходимо создать программный продукт при помощи Windows Forms на языке C#, который представлял бы возможность:
- ввода данных с клавиатуры или считывания их из файла с представлением права выбора пользователю;
- решения системы линейных уравнений;
- запись данных в файл;
- доступа к файлу, куда записываются входные и выходные данные.
Программа должна выполнять решение систем линейных уравнений методом Гаусса, методом Крамера или методом обратной матрицы.
Окно программы должно содержать:
- пункты меню: Файл, Правка, Примеры, Справка, О программе;
- поле выбора метода решения системы линейных уравнений;
- поле выбора количества уравнений в системе;
- поля для входных и выходных данных;
- кнопки операций.
Входными данными являются числа вещественного типа, введенные с клавиатуры или считанные из файла. Программа распознает входные данные и производит решение системы одним из выбранных методов.
Результатом работы программы служит отображение получившейся матрицы или определителя (в зависимости от выбранного способа) и корни системы уравнений, полученные в результате решения системы.
2 описание предметной области
Решение систем линейных алгебраических уравнений – одна из фундаментальных задач математики. Система m линейных алгебраических уравнений с n неизвестными (или, линейная система, также употребляется аббревиатура СЛАУ) в линейной алгебре - это система уравнений вида (Рисунок 1)
|
Рисунок 1- Система уравнений |
В системе уравнений (Рисунок 1) m является количеством уравнений, а n – количество неизвестных. x1, x2, … xn – это неизвестные, которые надо определить. a11, a12, … amn – коэффициенты системы, а b1, b2, … bm – свободные члены. Индексы коэффициентов (aij) системы обозначают номера уравнения (i) и неизвестного (j), при котором стоит этот коэффициент, соответственно.
Существуют следующие способы решения систем линейных уравнений:
– метод Гаусса;
– метод Крамера;
– метод обратной матрицы.
2.1 Метод Гаусса
Метод Гаусса – классический метод решения системы линейных алгебраических уравнений. Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе треугольного вида, из которой последовательно, начиная с последних (по номеру), находятся все переменные системы. Хотя в настоящее время данный метод повсеместно называется методом Гаусса, он был известен и до К.Ф. Гаусса. Первое известное описание данного метода приведено в китайском трактате «Математика в девяти книгах», составленном между первым веком до н. э. и вторым веком н. э.
Далее приведено более подробное описание метода. Пусть исходная система будет вида (Рисунок 2):
Рисунок 2 - Исходная система уравнений
На рисунке 2.1 указана матрица A, вектор x и вектор b. Матрицей А называется основная матрица системы, вектором x – столбец неизвестных, вектором – столбец свободных членов.
Рисунок 2.1 - Матрица A
Согласно свойству элементарных преобразований над строками, основную матрицу этой системы можно привести к треугольному (или ступенчатому) виду (эти же преобразования нужно применять к столбцу свободных членов), что показано на рисунке 2.2
Рисунок 2.2 - Матрица треугольного вида
При этом будем считать, что базисный минор (ненулевой минор максимального порядка) основной матрицы находится в верхнем левом углу, то есть в него входят только коэффициенты при переменных xj1, … , xjr.
Тогда переменные xj1, … , xjr называются главными переменными. Все остальные называются свободными.
Если хотя бы одно число βi ≠ 0, где i > r, то рассматриваемая система несовместна, то есть у неё нет ни одного решения.
Пусть βi ≠ 0 для любых i > r. Перенесём свободные переменные за знаки равенств и поделим каждое из уравнений системы на свой коэффициент при самом левом x (см. рисунок 2.3):
где
Рисунок 2.3- Несовместная система
Если свободным переменным системы (рисунок 2.3) придавать все возможные значения и решать новую систему относительно главных неизвестных снизу вверх (то есть от нижнего уравнения к верхнему), то мы получим все решения этой системы линейных алгебраических уравнений. Так как эта система получена путём элементарных преобразований над исходной системой, то по теореме об эквивалентности при элементарных преобразованиях системы (рисунок 2) и (рисунок 2.3) эквивалентны, то есть множества их решений совпадают.
2.2 Метод Крамера
Метода Крамера – способ решения систем линейных алгебраических уравнений с числом уравнений равным числу неизвестных с ненулевым главным определителем матрицы коэффициентов системы, причём для таких уравнений решение существует и единственно. Назван по имени Габриэля Крамера, предложившего этот метод в 1750 г.
Рисунок 2.4 - Система линейных уравнений
Для системы n линейных уравнений (рисунок 2.4) с n неизвестными с определителем матрицы системы ≠ 0, решение записывается по формуле показанном на рисунке 2.5:
Рисунок 2.5 - Нахождение решения
i-ый столбец матрицы системы заменяется столбцом свободных членов.
2.3 Метод обратной матрицы
Метод обратной матрицы – метод решения системы линейных алгебраических уравнений, использующий понятие обратной матрицы.
Обратная матрица – такая матрица A−1, при умножении на которую, исходная матрица A даёт в результате единичную матрицу E (формула 2.6).
(2.6)
Обратная матрица находится по формуле 2.7.
(2.7)
В формуле 2.7 det обозначает определитель.
Если необходимо решить систему линейных уравнений Ax = b, где b – ненулевой вектор, в который входят свободные члены, x – искомый вектор. Если обратная матрица A-1 существует, то x = A-1b. В противном случае либо размерность пространства решений больше нуля, либо их нет вовсе.
3 ПРОграммная реализация решения задачи
3.1 Введение и общие сведения
Одна из основных задач линейной алгебры – решение систем линейных алгебраических уравнений. Эта задача имеет важное прикладное значение при решении научных и технических проблем. Кроме того, является вспомогательной при реализации многих алгоритмов вычислительной математики, математической физики, обработки результатов экспериментальных исследований.
Программа «MATrix» предназначена для решения систем линейных алгебраических уравнений тремя методами:
- методом Гаусса;
- методом Крамера;
- методом обратной матрицы.
Данный программный продукт значительно упрощает получение корней систем линейных уравнений.
3.2 Структура программного продукта
В процессе разработки программного продукта были реализованы следующие формы:
- Formcs – форма приветсвия;
- MATrix.cs – форма, обеспечивающая решение систем линейных алгебраических уравнений методом Гаусса, методом Крамера или методом обратной матрицы по выбору пользователя;
- About.cs – форма, содержащая информацию о программном продукте.
На рисунке 3.1 изображена функциональная схема.
|
Форма приветствия |
|
Форма решения системы линейных уравнений |
|
Поле выбора метода |
|
Метод Гаусса
|
|
Метод Крамера
|
|
Метод обратной матрицы |
|
Поле выбора количества неизвестных |
|
Открыть значения из файла
|
|
Текстовый файл
|
|
Сохранить отчет
|
|
Файл |
|
Текстовый файл
|
|
Открыть значения из файла
|
|
Правка
|
|
Сохранить отчет
|
|
Меню |
|
Поле результата |
|
Примеры
|
|
О программе
|
|
Справка
|
|
#2 и |
|
#1 и |
Рисунок 3.1 – Функциональная схема программного продукта
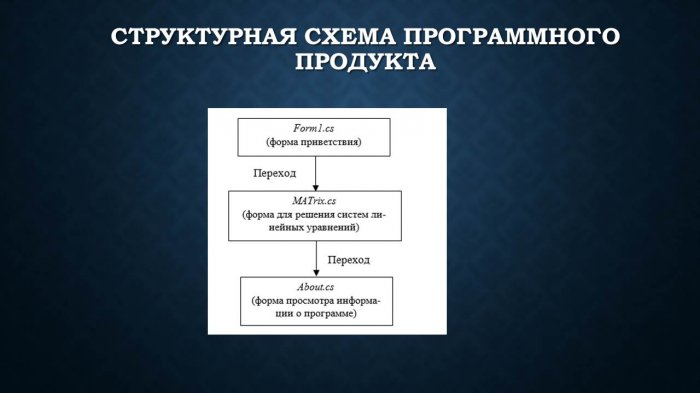
На рисунке 3.2 представлена структурная схема программы.
|
Переход |
|
Form1.cs |
|
MATrix.cs |
|
Переход |
|
About.cs |
Рисунок 3.2 – Структурная схема программного продукта
Во время работы дополнительных файлов приложение не использует.
3.3 Описание типов данных
В ходе работы приложение использует:
- двумерный массив MatrixA[,] типа double, в котором хранятся коэффициенты перед переменными;
- одномерный массив VectorB[] типа double, в котором хранятся свободные члены уравнений системы;
- одномерный массив VectorX[] типа double, элементы которого будут результатом решения системы;
- одномерный массив VectorU[] типа double – вектор невязки; переменную eps типа double, принимает значения порядка точности для сравнения вещественных чисел;
- переменную size типа int, которая задает количество неизвестных в системе уравнений;
- строковую переменную allElements, в которую считываются данные из файла.
3.4 Описание исходных текстов программного продукта
При работе с приложением были разработаны пользовательские обработчики событий и методы для форм Form1, MATrix, About, которые представлены ниже.
Обработчики событий Form1:
- okButton_Click(object sender, EventArgs e) – скрывает данную форму и производит переход на форму MATrix;
- button1_Click(object sender, EventArgs e) – закрывает приложение.
Методы и обработчики событий формы MATrix:
- TextBox InitTextBox(bool readOnly) – создает текстарию и назначает ему свойства;
- ValidateTextBox(object sender, CancelEventArgs e) – выполняет проверку текста;
- TextBox[,] InitTextBoxMatrix(TableLayoutPanel layoutPanel, int count, bool readOnly) – создает двумерный массив, вставляя каждую таблицу расположения;
- InitMatrixA() – создает поля для матрицы A размерности n*n;
- InitVectorB() – создает поля для матрицы B размерности n;
- int N – устанавливает размерность матриц;
- numericUpDown1_ValueChanged(object sender, EventArgs e) – дает возможность изменить размерность матрицы;
- button1_Click(object sender, EventArgs e) – получает и выводит результат решения системы линейных уравнений в richTextBox1;
- double[,] MatrixA – собирает матрицу A и записывает ее в текстбоксы;
- double[] VectorB – собирает вектор B и записывает его в текстбоксы;
- toolStripMenuItem2_Click(object sender, EventArgs e) – выводит значения в поля матрицы A и вектора B для примера с четырьмя неизвестными;
- toolStripMenuItem3_Click(object sender, EventArgs e) – выводит значения в поля матрицы A и вектора B для примера с четырьмя неизвестными;
- сохранитьКакToolStripMenuItem_Click(object sender, EventArgs e) – сохраняет результат выполнения программы в текстовый документ;
SaveFileDialog saveFileDialog = new SaveFileDialog();
saveFileDialog.Filter = "Текстовый документ (*.txt)|*.txt|Все файлы (*.*)|*.*";
if (saveFileDialog.ShowDialog() == DialogResult.OK)
{
StreamWriter FileOut = new StreamWriter(saveFileDialog.FileName, false, Encoding.GetEncoding("windows-1251"));
FileOut.WriteLine(richTextBox1.Text);
FileOut.Close();
}
- решитьToolStripMenuItem_Click(object sender, EventArgs e) – получает и выводит результат решения системы линейных уравнений в richTextBox1;
- button2_Click(object sender, EventArgs e) - сохраняет результат выполнения программы в текстовый документ;
SaveFileDialog saveFileDialog = new SaveFileDialog();
saveFileDialog.Filter = "Текстовый документ (*.txt)|*.txt|Все файлы (*.*)|*.*";
if (saveFileDialog.ShowDialog() == DialogResult.OK)
{
StreamWriter FileOut = new StreamWriter(saveFileDialog.FileName, false, Encoding.GetEncoding("windows-1251"));
FileOut.WriteLine(richTextBox1.Text);
FileOut.Close();
}
- очисткаПолейToolStripMenuItem_Click(object sender, EventArgs e) – очищает поля;
- оПрограммеToolStripMenuItem1_Click(object sender, EventArgs e) – открывает окно «О программе»;
About F = new About();
F.Show();
- справкаToolStripMenuItem_Click(object sender, EventArgs e) – открывает справку;
- button3_Click(object sender, EventArgs e) – осуществляет выход из приложения;
- выходToolStripMenuItem_Click(object sender, EventArgs e) – осуществляет выход из приложения;
- открытьЗначенияИзФайлаToolStripMenuItem_Click(object sender, EventArgs e) – открывает значения из файла, выбранного пользователем.
OpenFileDialog openFileDialog = new OpenFileDialog();
открытьЗначенияИзФайлаToolStripMenuItem.Click += new EventHandler(открытьЗначенияИзФайлаToolStripMenuItem_Click);
openFileDialog.Title = "Выберите файл";
openFileDialog.Filter = "Текстовые файлы|*.txt";
if (openFileDialog.ShowDialog() != DialogResult.OK)
return;
StreamReader FileIn = new StreamReader(openFileDialog.FileName);
allElements = FileIn.ReadToEnd();
Regex inEl = new Regex(@"\d+(,\d)?");
Match el = inEl.Match(allElements);
for (int i = 0; i < MatrixA.GetLength(0); i++)
{
for (int j = 0; j < MatrixA.GetLength(1); j++)
{
if (el.Success)
{
MatrixA[i, j] = double.Parse(el.ToString());
el = el.NextMatch();
}
else
{
MatrixA[i, j] = 0;
}
}
if (el.Success)
{
VectorB[i] = double.Parse(el.ToString());
el = el.NextMatch();
}
else
{
VectorB[i] = 0;
}
}
FileIn.Close();
richTextBox1.Clear();
Для нахождения корней системы линейных алгебраических уравнений был написан класс LinearSystem, методы которого приведены ниже:
- LinearSystem(double[,] a_matrix, double[] b_vector) : this(a_matrix, b_vector, 0.0001) – запоминает исходную матрицу A и исходный вектор B, с копиями которых будут производиться вычисления;
if (a_matrix == null || b_vector == null)
throw new ArgumentNullException("Один из параметров равен null.");
int b_length = b_vector.Length;
int a_length = a_matrix.Length;
if (a_length != b_length * b_length)
throw new ArgumentException(@"Количество строк и столбцов в матрице A должно совпадать с количеством элементров в векторе B.");
this.initial_a_matrix = a_matrix;
this.a_matrix = (double[,])a_matrix.Clone();
this.initial_b_vector = b_vector;
this.b_vector = (double[])b_vector.Clone();
this.x_vector = new double[b_length];
this.u_vector = new double[b_length];
this.size = b_length;
this.eps = eps;
GaussSolve();
- double[] XVector – получает значения вектора X;
get
{
return x_vector;
}
- double[] UVector – получает значения вектора U;
get
{
return u_vector;
}
- int[] InitIndex() – инициализирует массив индексов столбцов;
int[] index = new int[size];
for (int i = 0; i < index.Length; ++i)
index[i] = i;
return index;
- double FindR(int row, int[] index) – ищет главный элемент в массиве;
int max_index = row;
double max = a_matrix[row, index[max_index]];
double max_abs = Math.Abs(max);
for (int cur_index = row + 1; cur_index < size; ++cur_index)
{
double cur = a_matrix[row, index[cur_index]];
double cur_abs = Math.Abs(cur);
if (cur_abs > max_abs)
{
max_index = cur_index;
max = cur;
max_abs = cur_abs;
}
}
if (max_abs < eps)
{
if (Math.Abs(b_vector[row]) > eps)
throw new GaussSolutionNotFound("Система уравнений несовместна.");
else
throw new GaussSolutionNotFound("Система уравнений имеет множество решений.");
}
// меняем местами индексы столбцов
int temp = index[row];
index[row] = index[max_index];
index[max_index] = temp;
return max;
- GaussSolve() – находит решение системы линейных уравнений;
int[] index = InitIndex();
GaussForwardStroke(index);
GaussBackwardStroke(index);
GaussDiscrepancy();
- GaussForwardStroke(int[] index) - выполняет прямой ход метода Гаусса;
// перемещаемся по каждой строке сверху вниз
for (int i = 0; i < size; ++i)
{ // выбор главного элемента
double r = FindR(i, index);
//преобразование текущей строки матрицы А
for (int j = 0; j < size; ++j)
a_matrix[i, j] /= r;
// преобразование i-го элемента вектора b
b_vector[i] /= r;
// вычетание текущей строки из всех нижерасположенных строк
for (int k = i + 1; k < size; ++k)
{
double p = a_matrix[k, index[i]];
for (int j = i; j < size; ++j)
a_matrix[k, index[j]] -= a_matrix[i, index[j]] * p;
b_vector[k] -= b_vector[i] * p;
a_matrix[k, index[i]] = 0.0;
}
}
- GaussBackwardStroke(int[] index) – выполняет обратный ход метода Гаусса;
// перемещаемся по каждой строке снизу вверх
for (int i = size - 1; i >= 0; --i)
{ // создаётся начальное значение элемента х
double x_i = b_vector[i];
// корректировка этого значения
for (int j = i + 1; j < size; ++j)
x_i -= x_vector[index[j]] * a_matrix[i, index[j]];
x_vector[index[i]] = x_i;
}
- GaussDiscrepancy() – вычисляет невязку решения.
for (int i = 0; i < size; ++i)
{
double actual_b_i = 0.0; // результат перемножения i-строки
// исходной матрицы на вектор х
for (int j = 0; j < size; ++j)
actual_b_i += initial_a_matrix[i, j] * x_vector[j];
// i-й элемент вектора невязки
u_vector[i] = initial_b_vector[i] - actual_b_i;
}
В форме About применялся обработчик события button1_Click(object sender, EventArgs e), который обеспечивает закрытие формы.
3.5 Аппаратная и программная часть
Приложение «MATrix» было разработано в среде Microsoft Visual С# 2013 Pro на компьютере с 32-разрядной операционной системой Windows 8.1 Pro, который обладает следующими аппаратными характеристиками:
- процессор: Intel(R) Core(TM) i3-2370M CPU 2.40 GHz;
- RAM: 6.0 Gb;
- Intel: VRAM 1664 Mb.
Дополнительно применялись программы:
- Adobe Photoshop CC2.1 – графический редактор;
- Smart Install Maker04 – программа для создания инсталлятора;
- Dr.Explain – приложение для создания файлов справки.
3.6 Результаты тестирования и опытной эксплуатации
В ходе разработки программного продукта было произведено тестирование. После запуска программы необходимо выбрать «Далее» для перехода к форме решения систем линейных уравнений.
При вводе коэффициентов и свободных членов может быть введен не верный формат. В таком случае, после нажатии кнопки или пункта меню «Решить», ничего не произойдет. Результат тестирования можно увидеть на рисунке 3.3.
Рисунок 3.3 – Результат отработки с неверным форматом
При вводе верного формата программа верно находит решение системы уравнений. Результат решения системы линейных уравнений методом Гаусса изображен на рисунке 3.4.
Рисунок 3.4 – Результат решения системы методом Гаусса
Результаты решения системы линейных уравнений методом Крамера можно увидеть на рисунке 3.5.
Рисунок 3.5 – Результат решения системы методом Крамера
Полученное решение системы уравнений методом обратной матрицы изображено на рисунке 3.6.
Рисунок 3.6 – Результат решения системы методом обратной матрицы
При очистке поля результата решения системы поле успешно очищается при использовании любого способа. При сохранении результат сохраняется в файл, который пользователь может выбрать сам. Ошибок не возникает.
Тестирование данного программного продукта было пройдено успешно. Все ошибки были найдены и устранены.
4 РУКОВОДСТВО Пользователя
4.1 Введение
Программа «MATrix» разработана с целью упрощения решения систем линейных уравнений. Это приложение поможет пользователю решить систему линейных алгебраических уравнений методом Гаусса, методом Крамера или методом обратной матрицы.
4.2 Системные требования
Минимальные системные требования для корректной отработки программного продукта:
- процессор: Intel(R) Core(TM) i3-2370M CPU 2.40 GHz;
- версия .Net не ниже 3.0;
- RAM: 512 Mb;
- свободных 100 Mb на жестком диске.
4.3 Установка программного продукта
Для установки программного продукта, необходимо запустить файл Setup.exe. В начале установки необходимо указать папку для установки программы, а затем выбрать, где будут созданы ярлыки. После этого начнется процесс установки программного продукта на компьютер. По завершению установки запуск программы будет возможен, например, из меню «Пуск» или при нажатии на ярлык на Рабочем столе.
4.4 Запуск и работа с программным продуктом
Программа «MATrix» предназначена для решения систем линейных алгебраических уравнений методом Гаусса, методом Крамера и методом обратной матрицы.
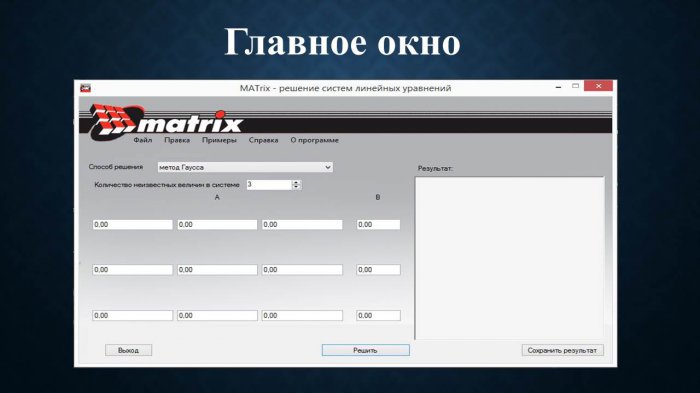
Запустить программу можно, нажав на ярлык на рабочем столе под названием «MATrix» или в меню «Пуск». При запуске открывается главное окно, представленное на рисунке 4.1.
Рисунок 4.1 – Главное окно программы
На главном окне программы присутствуют две кнопки: «Далее» и «Выход». Также описано, для чего предназначена программа. Для непосредственной работы с приложением нужно выбрать режим и нажать кнопку «Далее». Если программа запущена случайно, можно нажать «Выход», после чего приложение полностью закроется.
На рисунке 4.2 представлено окно, в котором происходит решение системы линейных алгебраических уравнений.
Рисунок 4.2 – Окно решения систем линейных уравнений
По умолчанию выбран метод Гаусса с системой линейных уравнений с тремя неизвестными. По желанию также можно выбрать метод Крамера или метод обратной матрицы и выбрать нужное количество неизвестных.
Чтобы решить систему уравнений, необходимо ввести коэффициенты перед неизвестными и свободные члены, после чего нажать кнопку или пункт меню «Решить». Чтобы не вводить коэффициенты вручную, можно считать их из файла, для чего нужно выбрать пункт меню «Файл» и подпункт «Открыть значения из файла». Далее для решения нужно нажать кнопку или пункт меню «Решить».
В правом поле будет выведен результат отработки программы, то есть будут найдены и выведены корни системы уравнений. Отчет можно сохранить в текстовый документ, нажав на кнопку или пункт меню «Сохранить результат.
Кликнув пункт меню «О программе» выйдет окно, в котором можно увидеть краткое описание программы, ее версию, разработчика и год вышедшей версии. Окно «О программе» можно увидеть на рисунке 4.3.
Рисунок 4.3 – Окно «О программе»
Также можно открыть справку, в которой подробно описана работа с программой «MATrix».
4.5 Удаление программного продукта
Для удаления программного продукта, необходимо зайти в Панель управления компьютера и выбрать категорию «Установка и удаление программ». После этого на экране появится список установленных на данный компьютер программ, где необходимо найти программу «MATrix», выбрать ее и нажать на кнопку «Удалить». Также программу можно удалить инсталлятором, который находится в каталоге, указанном пользователем при установке программного продукта.
ЗАКЛЮЧЕНИЕ
В ходе курсовой работы было разработано готовое приложение «MATrix» для решения систем линейных алгебраических уравнений методом Гаусса, методом Крамера и методом обратной матрицы. В качестве языка разработки был выбран язык программирования высокого уровня С#. В качестве среды разработки была выбрана Microsoft Visual Studio 2013. Демонстрация работы программного модуля реализована с помощью графического интерфейса (Windows Forms).
В курсовой работе были решены следующие задачи:
- Изучены три основных способа решения систем линейных алгебраических уравнений.
- Реализован алгоритм решения систем линейных алгебраических уравнений медом Гаусса, методом Крамера и методом обратной матрицы.
- Разработан программный продукт, протестирован и отлажен.
Все поставленные задачи в курсовой работе решены, цель достигнута.
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
- MSDN. Справочные материалы по C# [Электронный ресурс]. – 2014. – Режим доступа: http://msdn.microsoft.com/ru-ru/library/618ayhy6.aspx
- Агуров П. В. С# сборник рецептов.-СПб.: БВХ-Петербург.2007.-432 с.
- Красиков И. В. Алгоритмы. Просто как дважды два. –М.: Эксмо, 2007. -256с.
- Мартынов Н. Н. С# для начинающих. КУДИЦ-ПРЕСС,Москва,2007. Тираж 2000. Заказ 1428. - 272 с.
- Метод Гаусса [Электронный ресурс]. – 2014. – Режим доступа: http://ru.wikipedia.org/wiki/Метод_Гаусса/
- Метод Крамера [Электронный ресурс]. – 2014. – Режим доступа: http://ru.wikipedia.org/wiki/Метод_Крамера/
- Метод обратной матрицы [Электронный ресурс]. – 2014. – Режим доступа: http://www.testent.ru/publ/studenty/vysshaja_matematika/metod_obratnoj_matricy_matrichnyj_metod/35-1-0-1048
- Нейгел, Кристиан, Ивьен, Билл, Глини, Джей, Уотсон, Карли. С#0 и платформа .NET 4 для профессионалов.:Пер. с англ. –М.:ООО”И.Д.Вильямс”,2011. – 1440 с.
- Обратная матрица [Электронный ресурс]. – 2014. – Режим доступа: http://ru.wikipedia.org/wiki/Обратная_матрица/
- Фаронов В. В. Программирование на языке C#.СПб.: Питер,2007.-240с.
- Шилдт Г. Полный справочник по С#.: Пер. с англ. – М. : Издательский дом «Вильямс»,
Презентация
Скачать: