Метрологическое обеспечение исследований средств измерения параметров зашумленных доплеровских сигналов

Кафедра промышленной электроники и информационной

измерительной техники

ДИПЛОМНАЯ РАБОТА

Метрологическое обеспечение исследований средств измерения параметров зашумленных доплеровских сигналов

Пояснительная записка

Аннотация

Пояснительная записка содержит 85 страниц, в том числе 14 рисунков, 5 таблиц, 1 приложение. Графическая часть выполнена на 6 листах формата A1.

В дипломной работе разработано программное средство для воспроизведения моделей зашумленного доплеровского сигнала приближенного по параметрам к реальным доплеровским сигналам. В работе проводились экспериментальные исследования отдельных составляющих модели и погрешности ее воспроизведения.

Программное средство предназначено для метрологического обеспечения исследований при совершенствовании средств измерения доплеровских сигналов. Основные технико-эксплуатационные показатели: высокая точность воспроизведения при больших значениях первой и второй производных частот доплеровских колебаний в условиях шума, воспроизведенного с параметрами, близкими к белому шуму. Эффективность разработанного метрологического средства определяется небольшими затратами при высокой адекватности реальным доплеровским сигналам.

Дипломная работа содержит расчет экономических показателей, рассмотрены вопросы безопасности труда.

Summary

The Explanatory note contains 85 pages, including 16 drawings, 6 tables, 1 exhibit. The Graphic part was run for 6 sheets of the format A1.

Software programs is designed In degree work for reproducing the models зашумленного доплеровского of the signal drawn near on parameter to real доплеровским signal. In work were conducted experimental studies separate forming models and inaccuracy of her(its) reproduction.

Software programs is intended for metrological ensuring the studies at improvement of the facilities of the measurement доплеровских signal. The Main technician-working factors: pinpoint accuracy of the reproduction under greater importances first and the second derived frequencies доплеровских fluctuations in condition of the noise, reproduced with parameter, close to white noise. Efficiency designed metrological facility is defined small expenses under high adequacy real доплеровским signal.

Degree work contains the calculation of the economic factors, considered questions to safety of the labour.

Содержание

Введение………………………………………………………………………..5
1. Анализ задачи исследования ……………………………………………….6
1.1 Общая характеристика ДИИС……………………………………….6 1.2 Оценка шумовой помехи в ДИИС…………………………………..9 1.3 Квантование и дискретизация сигналов в ДИИС………………….14 1.4 Формулирование задач исследования………………………............18 2. Разработка средства воспроизведения зашумленных доплеровских сигналов……………………………………………………….20
2.1 Модель доплеровского колебания ………………………………….21
2.2 Модель генератора шума…………………….....................................25
2.2.1 Линейная конгруэнтная последовательность………………..27 2.2.2 Генерация ПСП библиотечной функцией……………………28 2.2.3 Генерация ПСП на основе последовательности Фибоначчи с запаздыванием……………………………………………….28 2.2.4 Генерация ПСП на основе регистра сдвига с обратными связями…………………………………………………………..29 2.2.5. Анализ алгоритмов ПСП, не включенных в модель доплеровского сигнала……………………………………………..31 2.2.6 Метод перемешивания…………………………………………32
2.3 Статистические тесты на случайность……………………………...33 2.3.1 Монобитный тест………………………………………………34 2.3.2 Покер-тест………………………………………………………35 2.3.3 Серийный тест………………………………………………….36 2.3.4 Тест «Длинные цепочки»……………………………………...37 2.3.5 Автокорреляционный тест………………………….…………38 2.4 Модель дискретного доплеровского сигнала………………………39
3. Экспериментальные исследования ………………………………………..42 3.1 Модель шумовой помехи…………………………………………………42 3.2 Метрологическая аттестация моделей доплеровского сигнала…...45
4. Экономический расчет проекта……………………………………………48
5. Безопасность труда………………………………………………………….54
Заключение…………………………………………………………………….64
Список использованных источников………………………………………..65
Приложение А (Справочное) - …………………….68

Введение

Для решения задач внешней баллистики, занимающейся исследованием движения летательных объектов малых размеров, большое значение имеет повышение точности измерения траекторных характеристик, что непосредственно связано с повышением разрешающей способности по дальности и скорости соответствующих наземных радиотехнических информационно-измерительных систем [6,15,52,85,106]. К таковым системам относится класс доплеровских информационно-измерительных систем (ДИИС) с непрерывным облучением удаляющегося летательного объекта малых размеров в гигагерцовом диапазоне частот.

Повышение разрешающей способности обозначенного класса систем связано с обеспечением метрологическими средствами как существующие, так и разрабатываемые средства измерительной обработки зашумленных доплеровских сигналов, входящие в состав ДИИС. Эффективное проведение исследований в рамках сформулированной тематики с учетом требований к системам невозможно без моделирования. Создание метрологического средства на основе моделей зашумленных доплеровских колебаний является обязательным компонентом в комплексной разработке методов и средств распознавания и измерения параметров доплеровских колебаний.

Целью дипломной работы является метрологическое обеспечение доплеровских информационно-измерительных систем тестовыми сигналами, приближенными по параметрам к реальным доплеровским сигналам. Метрологическое обеспечение основано на воспроизведении модели зашумленного доплеровского сигнала с детерминированными параметрами. Для воспроизведения модели доплеровского сигнала, адекватной реальным доплеровским сигналам, в модели должны отражаться требования, предъявляемые к разрешающей способности и точности ДИИС, особенностям полетных характеристик летательных объектов, характера шума и динамики соотношения «сигнал/шум».

Главное назначение моделей зашумленных доплеровских колебаний как средств воспроизведения – метрологическая оценка разрабатываемых методов и средств обработки зашумленных доплеровских сигналов в части разрешающей способности обнаружения доплеровского колебания в смеси с шумом и точности измерения мгновенных значений угловой частоты обнаруженного доплеровского колебания.

1 Анализ задачи исследования

1.1 Общая характеристика ДИИС

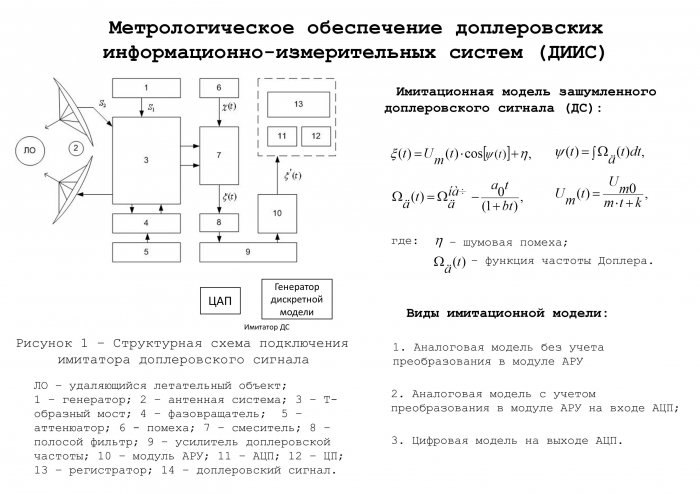
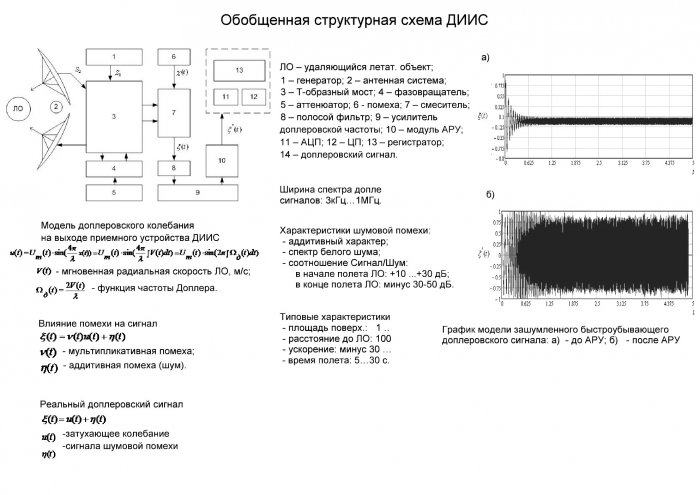
Обобщенная структурная схема современных ДИИС изображена на рисунке 1.1 [3,12,19].

Рисунок 1.1 – Обобщенная структурная схема ДИИС: ЛО – летательный объект; 1 – генератор; 2 – антенная система; 3 – Т-образный мост; 4 – фазовращатель; 5 – аттенюатор; 6 - помеха; 7 – смеситель; 8 – полосой фильтр; 9 – усилитель доплеровской частоты; 10 – модуль автоматической регулировки усиления; 11 – аналого-цифровой преобразователь; 12 – цифровой процессор; 13 – регистратор.

В системе ДИИС электромагнитные колебания, излучаемые генератором (1), поступают на двойной Т – образный мост (3) и делятся на два луча – измерительный и опорный . Антенная система (2), являющаяся приемопередающей, направляет измерительный луч на исследуемый объект (ЛО) и принимает отраженный луч. Опорный луч и измерительный луч соответственно можно представить в виде мгновенных значений напряжений:

где: ;

- геометрическая длинна луча;

- длинна электромагнитной волны.

Геометрическая длина луча содержит информацию о расстоянии до движущегося летательного объекта. С помощью двойного Т - образного моста (3) измерительный луч направляют в смесительную секцию (7), где происходит сложение с опорным лучом, амплитуда и фаза которого зависят от фазовращателя (4) и аттенюатора (5), которые предназначены для выбора оптимального режима работы смесительной секции. В смесительной секции происходит перемножение опорного и измерительного лучей и преобразование интерференционной картины в электрическое колебание:

Из последнего выражения видно, что на выходе смесительной секции электрическое колебание представляет собой сумму двух колебаний. Первое колебание, фаза которого прямо пропорциональна частоте опорного луча, является высокочастотным, второе колебание, фаза которого зависит только от геометрической длины луча, является низкочастотным. После выделения низкочастотной составляющей получают (доплеровское) колебание вида:

где: ;

- амплитуда колебания;

- базовая длинна луча;

- текущее расстояние до ЛО;

По мере удаления ЛО от антенн ДИИС при мощность принятого радиолокационного сигнала на входе приемного устройства (3) затухает по закону, выраженному зависимостью [21]:

где: - мощность передатчика;

- коэффициент направленного действия антенны;

- эффективная площадь рассеяния цели;

- эффективная площадь антенны.

На выходе смесительной секции уровень амплитуды доплеровского колебания, пропорциональный мощности принятого радиолокационного сигнала, , представляется согласно зависимости:

где: ;

- затухание уровня амплитуды колебания по мере удаления ЛО от антенн ДИИС.

С помощью фазовращателя (4) значение начальной фазы устанавливают так, чтобы при нахождении ЛО в неподвижном положении значение напряжения на выходе низкочастотного блока равнялось нулю, то есть .

В результате модель доплеровского колебания на выходе приемного устройства ДИИС имеет вид:

(1.1)

где: - мгновенная радиальная скорость ЛО, м/с;

- функция частоты Доплера.

С выхода приемного устройства (рисунок 1.1) доплеровское колебание подвергается предварительной обработке: пропускают через полосовой фильтр (8), усиливают в УДЧ (9) и нормируют его уровень по эффективному значению в модуле АРУ (10) [20], обеспечивая размах амплитуды сигнала в диапазоне полной шкалы АЦП. С выхода АРУ доплеровский сигнал посредством АЦП представляют в цифровом виде. Цифровые выборки загружают в ЭВМ, где их обрабатывают и получают функцию частоты Доплера (скорости) в течение полета ЛО малых размеров. Для современных ДИИС обозначенного класса типовой диапазон измеряемых значений частоты Доплера оценивается интервалом от 3 кГц до 1 МГц. Погрешность измерения не более 0,5% [3,25,26].

1.2 Оценка шумовой помехи в ДИИС

В реальных доплеровских сигналах кроме измерительной информации в сигнале содержится помеха [1,6,15,25]. На выходе приемного устройства доплеровский сигнал представляет собой смесь информативного доплеровского колебания (1.1) и сигнала шумовой помехи. В общем виде влияние помехи на сигнал может быть выражено оператором :

где: - мультипликативная помеха;

- аддитивная помеха (шум).

Основными источниками аддитивных помех являются внутренние шумы активных элементов, имеющих тепловую или иную природу (фликкер-шумы, тепловой, дробовой шум). Мультипликативная составляющая помехи обусловлена в основном нестабильностью передаточных функций элементов информационных каналов, вызываемых внешними воздействиями: климатическими, механическими и другими. Дополнительным источником мультипликативной помехи является также модуль АРУ [20]. Сигнал на выходе АРУ можно представить:

где: - нормируемый коэффициент усиления;

В результате воздействия АРУ на сигнал, добавляется флуктуирующая по интенсивности аддитивная помеха. Хотя модуль АРУ вносит дополнительную помеху в измерительный процесс, используя автоматическую регулировку усиления сигнала по эффективному значению (для стационарных случайных процессов), обеспечивается полный размах амплитуды сигнала в диапазоне полной шкалы АЦП (рисунок 1.2). Погрешность квантования сохраняется по величине и составляет менее ±0,05%.

а)

б)

Рисунок 1.2 – График модели зашумленного быстроубывающего

доплеровского сигнала: а) - до АРУ; б) - после АРУ

В современных ДИИС обозначенного класса в частотном диапазоне от 3кГц до 1МГц влияние аддитивной составляющей помехи существенно преобладает над ее мультипликативной составляющей [3,21]. В целом реальный доплеровский сигнал на выходе приемного устройства ДИИС представляет собой преимущественно аддитивную смесь затухающего колебания с доплеровской частотой и сигнала шумовой помехи :

Преобладающими источниками аддитивных помех в системах ДИИС, как правило, являются активные элементы СВЧ приемника [3,21]. К основным источниками, определяющими характер шума в СВЧ приемнике, относят антенную систему (АС), усилитель высокой частоты (УВЧ), смеситель частоты (СМ) и усилитель доплеровской частоты (УДЧ) (рисунок 1.1). Количественно шумовые свойства этих элементов определяются коэффициентом шума . Коэффициент шума показывает, насколько элемент (группа элементов) ухудшает соотношение сигнал/шум:

где: - сигнал/шум на входе элемента;

- сигнал/шум на выходе;

Для минимизации влияния шума радиоприемные устройства должны иметь достаточную избирательность, необходимое усиление и низкий коэффициент шума. Для получения минимального коэффициента шума в составе приемника, как правило, предусматривается усилитель высокой частоты (УВЧ). В усилителях УВЧ широко используются схемы на УВЧ транзисторах и туннельных диодах. Это связано с тем, что такие усилители имеют низкий уровень шумов, простую конструкцию и не требуют сложных дополнительных технических средств, таких как генераторы накачки и холодильные устройства. Оценки показывают [7,23], что типовые значения коэффициента шума для УВЧ, построенных по транзисторной схеме, ограничиваются величиной в 2 – 5 дБ, для УВЧ построенных по схеме на туннельных диодах - величиной в 2 - 3 дБ. Избирательность УВЧ достигается за счет использования реактивных элементов [3]. Самое большое распространение в качестве СВЧ фильтров нашли микрополосковые фильтры. В таких элементах роль реактивных элементов играют короткозамкнутые или разомкнутые отрезки микрополосковых линий (МПЛ), которые при длине эквивалентны соответственно индуктивностям или емкостям.

Другим источником аддитивных помех является смеситель частоты (СМ). В диапазоне СВЧ, где не применимы электронные лампы для преобразования частоты, ранее применялись кристаллические смесители и гетеродин на клистроне. Коэффициент передачи такого смесителя меньше единицы при минимальном коэффициенте шума в 6 - 8 дБ, причем довольно трудно получить достаточно широкую полосу пропускания [7,23]. Появившиеся позднее параметрические преобразователи, действие которых основано на использовании нелинейной емкости, обладают меньшим уровнем шума и повышенным коэффициентом передачи. Однако параметрическим преобразователям, работающим при относительно низких промежуточных частотах, свойственен большой коэффициент шума. Параметрический преобразователь, понижающий частоту в 10 раз, имеет дополнительный коэффициент шума в 10 дБ. Кроме того, параметрический преобразователь является более сложным устройством, так как он требует внешнего генератора накачки, холодильного устройства и д.р. В настоящее время, в основном используются преобразователи на транзисторах, либо на туннельных диодах, которые обеспечивают большой коэффициент передачи при малом коэффициенте шума и широкой полосе пропускания. Коэффициент шума таких смесителей оценивается величиной в 2 - 3 дБ [3,7,23].

Шумы в антенной системе вызваны тепловым шумом собственного сопротивления антенны. Когда входной импеданс приемника согласован с импедансом антенны, в антенне расходуется половина мощности и коэффициент шума оценивается величиной в 2 - 3 дБ.

Шумы в обозначенных ранее устройствах, вызванные, в основном, внутренними шумами активных элементов (электронные лампы, транзисторы, туннельные диоды), можно представить в виде трех составляющих: дробовой, тепловой и мерцательный шум [10].

Тепловой шум обусловлен тепловым движением носителей заряда, приводящий к появлению случайной разности потенциалов. Он представляет собой случайный процесс с нулевым средним и спектральной плотностью мощности равной: , где , , - абсолютная температура источника, - частота. В диапазоне частот до 10 МГц (граничная частота ПФ) выполняется условие , спектральная плотность мощности равна: . Тепловой шум в обозначенном частотном диапазоне рассматривается как случайный процесс с нулевым средним и равномерной спектральной плотностью интенсивности .

Дробовой шум представляет собой флуктуирующие колебания напряжений и токов относительно их среднего значения в цепях радиоэлектронных устройств, обусловленные дискретностью носителей электрического заряда. Согласно [10] спектральная плотность дробового шума имеет сплошной равномерный спектр до весьма высоких частот (до нескольких МГц) и может быть приблизительно оценена выражением (формула Шоттки): , где - протекающий ток, - величина заряда электрона.

В диапазоне звуковых частот появляется составляющая шума, спектральная плотность которой убывает по закону . Это так называемый мерцательный шум, связанный с токами утечки переходов и д.р. На частотах свыше эта шумовая компонента пренебрежимо мала по сравнению с другими [7,10]. Поскольку измерение частот Доплера лежит выше обозначенного частотного диапазона, то этой составляющей шумовой помехи можно пренебречь.

В целом, в рассматриваемом частотном диапазоне шумовую помеху с достаточной степенью точности можно аппроксимировать стационарным случайным процессом с нулевым средним и спектром белого шума. На выходе полосового фильтра (рисунок 1.1) энергетический спектр шумовой помехи ограничивается в полосе пропускания приемного тракта :

где: - спектральная плотность шумового процесса.

Корреляционная функция такого процесса имеет вид:

Дисперсия (средняя мощность) такого процесса, равна:

Нормированная корреляционная функция процесса соответствует:

. (1.2)

Согласно теореме Котельникова реализация случайного процесса с ограниченным спектром полностью определяется выборкой случайных величин, представляющих его дискретные отсчеты через интервалы . Согласно (1.2) при нормированная корреляционная функция такого процесса , отсчеты через равномерные интервалы , полностью определяющие случайный стационарный процесс с равномерным энергетическим спектром, будут некоррелированные.

Обобщая, шумовую помеху в рассматриваемом классе ДИИС можно охарактеризовать аддитивным случайным стационарным процессом с нулевым средним, релеевским законом распределения плотности вероятности [3,15,21] и спектром белого шума в области измеряемых частот Доплера.

По отношению к измерительному процессу воздействие шумовой помехи на доплеровский сигнал ограничивает потенциальную возможность по разрешающей способности распознавания и точности измерения параметров доплеровского колебания. Динамику разрешающей способности распознавания параметров доплеровского сигнала на фоне шумовой помехи отражает соотношение «сигнал/шум» (С/Ш). Граничное значение соотношения С/Ш, при котором возможно безошибочное распознавание параметров доплеровского сигнала, отражает потенциал разрешающей способности ДИИС по дальности [3,21]. Для современных ДИИС уровень соотношения С/Ш по мере удаления ЛО малых размеров от облучаемых антенн ДИИС достигает значения минус 35…50 дБ [1,25,26.].

1.3 Квантование и дискретизация сигналов в ДИИС

В соответствии с ориентацией современных ДИИС на цифровую обработку доплеровских сигналов, их квантование и дискретизация во времени являются неотъемлемой частью преобразовательного процесса.

Главным и существенным отличием непрерывной по размеру величины от квантованной заключается в том, что первая в заданном диапазоне может иметь бесконечное число размеров, в то время как квантованная по размеру величина может иметь в заданном диапазоне только ограниченное число размеров. Разность между соседними заданными значениями квантованной величины называют ступенью квантования , где , - соседние уровни квантования. Различают квантование с равномерными и неравномерными размерами ступеней квантования. Для квантования с равномерными размерами ступеней , где - размах доплеровского сигнала; ; - количество уровней АЦП. В современных ДИИС в подавляющих случаях используются средства АЦП с равномерными размерами ступеней квантования.

Процедуры квантования и дискретизации доплеровских сигналов неизбежно вносят методическую погрешность в измерительный процесс. Погрешность квантования сигнала является погрешностью метода отражения непрерывной по размеру величины ограниченным по числу размеров числом , . Максимальная погрешность квантования зависит от способа отождествления сигнала с уровнем квантования. При отождествлении доплеровского сигнала с верхним или нижним значением уровня квантования погрешность равна соответственно размеру ступени, то есть . При отождествлении доплеровского сигнала ближайшим значением уровня квантования (путем введением цифровой поправки ) погрешность равна .

Оценку статистических характеристик погрешности квантования зашумленного доплеровского сигнала с законом распределения вероятности можно произвести следующим образом. При большом числе ступеней квантования можно предположить, что значение плотности вероятности случайного процесса внутри - ой ступени квантования постоянно, то есть [79], где . Математическое ожидание погрешности квантования зашумленного доплеровского сигнала на - ой ступени равно:

где: , - нижняя (верхняя) граница - ой ступени квантования.

Если отождествить с серединой ступени квантования, , тогда математическое ожидание погрешности квантования . Дисперсия погрешности квантования зашумленного доплеровского сигнала на - ой ступени равна:

Если отождествить с серединой ступени квантования, при , тогда дисперсия равна:

Дисперсия погрешности квантования с равномерными размерами ступеней, с учетом изменения доплеровского сигнала во всем диапазоне :

, (1.3)

Выражение (1.3) отражает значение дисперсии погрешности квантования с равномерными размерами ступеней при и любом законе распределения зашумленного доплеровского сигнала. Например, при количестве разрядов АЦП дисперсия погрешности квантования доплеровского сигнала не превысит значения 4,96×10^-9, а эффективное значение шума квантования: .

Дискретизация сигнала является измерительным преобразованием непрерывного сигнала в последовательность мгновенных значений этого сигнала , соответствующим определенным моментам времени :

где: - функция отсчетов;

- частота дискретизации;

Основополагающей теоремой теории дискретного представления сигналов является теорема Котельникова. В соответствии с этой теоремой возможно со сколь угодно высокой точностью восстановить любой непрерывный случайный процесс по его дискретным выборкам при следующих условиях:

- процесс имеет ограниченный спектр ;

- процесс наблюдается бесконечное время;

- выборки сообщения формируются с частотой опроса ;

- восстановление процесса ведется по значениям выборок в форме ряда Котельникова:

Реальные сигналы в ДИИС имеют конечную длительность. Спектр таких сигналов не ограничен, реальные сигналы не соответствуют в точности модели сигнала с ограниченным спектром, и применение теоремы Котельникова к реальным сигналам связано с погрешностями при восстановлении сигналов и неопределенностью выбора шага дискретизации или частоты отсчетов. Для практических условий, как правило, идеально точное восстановление функций не требуется, необходимо лишь восстановление с заданной точностью . Поэтому теорему Котельникова можно рассматривать как приближенную для функций с неограниченным спектром.

На практике частоту дискретизации доплеровских сигналов определяют в зависимости от заданной погрешности аппроксимации при известных значениях максимумов производных (вплоть до ), либо по автокорреляционной функции . Способы определения частоты дискретизации при различных методах восстановления сигнала систематизированы и приведены на рисунке 1.3.

Процедуры квантования и дискретизации позволяют представить непрерывный доплеровский сигнал последовательностью (комбинацией) двоичных цифр, которую уже можно непосредственно вводить в ЭВМ.

Рисунок 1.3 – Систематизация способов определения

частоты дискретизации.

2 Разработка средства воспроизведения моделей зашумленного доплеровского сигнала

При воспроизведении доплеровского сигнала необходимо учитывать преобразование формы доплеровского сигнала в каналах измерительного преобразования ДИИС (рисунок 1.1). На рисунке 2.1 изображена структурная схема аттестации отдельных узлов ДИИС посредством генератора модели доплеровского сигнала с учетом преобразования формы сигнала.

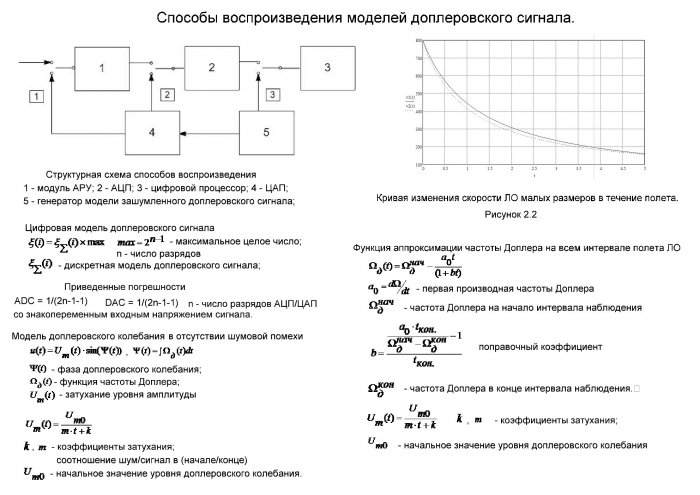
Рисунок 2.1 - Структурная схема подключения к узлам ДИИС средства воспроизведения зашумленного доплеровского сигнала: 1 – модуль АРУ; 2 – АЦП; 3 – цифровой процессор; 4 – ЦАП; 5 – генератор модели зашумленного доплеровского сигнала; в квадратиках обозначены виды воспроизводимой модели

Обозначенным способом [13] воспроизведения получают следующие виды сигнала:

аналоговую модель доплеровского сигнала без учета преобразования в модуле АРУ;
аналоговую модель доплеровского сигнала с учетом преобразования в модуле АРУ на входе АЦП;
цифровую модель доплеровского сигнала на выходе АЦП.

Воспроизведение моделей доплеровского сигнала реализуется в виде цифрового массива чисел – выборок из сформированной функции образа доплеровского сигнала. Использование такого подхода продиктовано рядом обстоятельств. Цифровым способом реализуется высокая точность вычислений, высокая стабильность характеристик, цифровая аппаратура не требует настройки и позволяет легко осуществлять адаптацию воспроизводимого сигнала к устройству. Поскольку современные ДИИС в каналах обработки доплеровских сигналов содержат АЦП, то подобный подход вполне корректен.

Цифровая модель доплеровского сигнала представляется в виде массива чисел в диапазоне [-max, +max]:

, (2.1)

где: - дискретная модель доплеровского сигнала;

– максимальное целое число;

n – число разрядов (для ЭВМ используемых в ДИИС ).

Приведенная погрешность представления доплеровского сигнала в третьем виде определяется выражением:

d_A_DC= 1/(2ⁿ^-1-1),

где n – число разрядов АЦП со знакопеременным входным напряжением сигнала.

Для воспроизведения первого и второго видов доплеровского сигнала используется цифро-аналоговое преобразование цифровой модели (2.1). Частота дискретизации в воспроизводимом доплеровском сигнале определяется как , где - ширина спектра доплеровского сигнала (от 3кГц до 1МГц). Приведенная погрешность аналогового представления доплеровского сигнала определяется выражением: d_D_A_C= 1/(2ⁿ^-1-1), где n – число разрядов ЦАП со знакопеременным входным напряжением сигнала.

2.1 Модель доплеровского колебания

Согласно (1.1) модель доплеровского колебания на выходе приемного устройства ДИИС в отсутствии шумовой помехи имеет вид:

, , (2.2)

где: - фаза доплеровского колебания;

- функция частоты Доплера;

- затухание уровня амплитуды сигнала вследствие удаления ЛО от антенн ДИИС.

Анализ полетных характеристик ЛО малых размеров [1,25,26] и зарегистрированных доплеровских сигналов в реальных ДИИС, полученных для удаляющихся по инерции (свободный полет) ЛО малых размеров на конечном интервале времени, получивших положительное ускорение в первый момент времени полета, показал следующее:

1) в начале интервала наблюдения преобладание энергии доплеровского колебания над помехой достигают: +30 дБ;

2) в конце интервала наблюдения преобладание помехи над доплеровским колебанием может достигать: +30…+50 дБ;

3) при отсутствии форсажа по скорости у ЛО малых размеров в процессе полета:

- в начале полетного времени существенное влияние на функцию доплеровской частоты оказывает вторая производная доплеровской частоты;

- в конце полетного времени основной вклад в изменение доплеровской частоты оказывает ее первая производная.

На основании проведенного анализа в источнике в источнике было установлено, что затухание частоты доплеровского колебания по мере удаления ЛО малых размеров от антенн ДИИС происходит по закону, близкому к обратному от времени полета закону. Наиболее точной аппроксимацией функции доплеровской частоты для указанных выше ЛО малых размеров оказалась аппроксимация в виде следующей зависимости, учитывающей как первую, так и вторую производные, убывающие по абсолютной величине в зависимости от времени t полета:

, (2.3)

где: – первая производная частоты Доплера в момент начала экстенсивной части полета ЛО малых размеров;

- частота Доплера на начало интервала наблюдения ,

Поправочный коэффициент рассчитывается как:

где: - частота Доплера на конце интервала наблюдения.

Рисунок 2.2 - Кривая изменения скорости ЛО малых размеров в течение полета.

На рисунке 2.2 изображены графики кривой изменения радиальной скорости в течение полета ЛО малых размеров. Графиком обозначено изменение скорости реального ЛО малых размеров, а графиком скорость, полученная с учетом выражения (2.3). Из сравнения этих графиков можно сделать вывод, что график имеет отклонение от не более 10% и полностью отражает характер поведения функции частоты Доплера, отраженного в .

Реальный сигнал на выходе приемного устройства ДИИС в диапазоне измеряемых частот Доплера 3кГц…1МГц представляет собой аддитивную смесь затухающего колебания с доплеровской частотой (2.3) и сигнала помехи :

При решении задач метрологической аттестации ДИИС интерес представляет случай, когда полезный сигнал маскируется уровнем шума [5]. Модель доплеровского сигнала должна отражать динамику соотношения С/Ш по мере удаления ЛО малых размеров от антенн ДИИС. На основании соотношения (2.2) и проведенного анализа было установлено, что затухание уровня (амплитуды) доплеровского колебания по отношению к шуму по мере удаления ЛО малых размеров от антенн ДИИС происходит по закону, отраженному аппроксимирующей зависимостью (рисунок 2.3):

, (2.4)

где: , – коэффициенты затухания; первый коэффициент отражает соотношение шум/сигнал в начале траектории ЛО малых размеров, второй коэффициент, определяет соотношение шум/сигнал в конце интервала наблюдения ;

– начальное значение уровня доплеровского колебания.

Поскольку модель доплеровского сигнала нужна в первую очередь для метрологической оценки средств обнаружения и измерения доплеровской составляющей отраженного сигнала от ЛО малых размеров, удаляющегося от антенн облучающей ДИИС, то подобная аппроксимация по частоте и амплитуде является вполне обоснованной и допустимой, так как главным ее свойством является:

детерминированность доплеровского колебания;
воспроизведение полетного закона соотношения сигнал/шум доплеровского сигнала;

- воспроизведение начального и конечного значений доплеровского колебания.

Рисунок 2.3 – График затухания уровня доплеровского колебания

2.2 Модель генератора шума

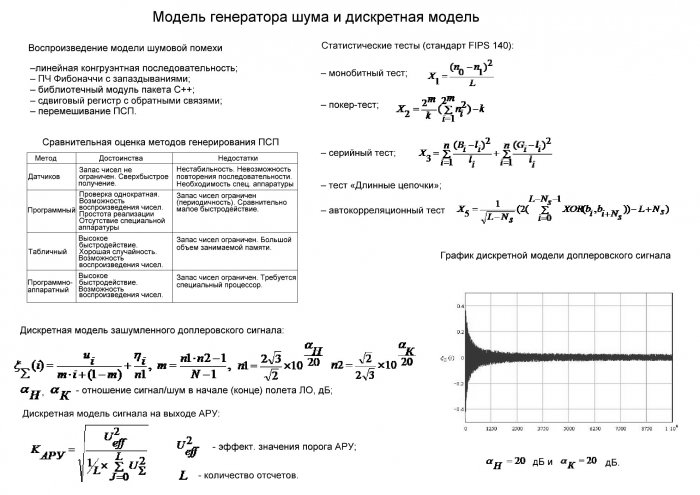
В реальных ДИИС сигнал шумовой помехи по своим характеристикам является близким к случайным стационарным процессам со спектром белого шума, ограниченным в диапазоне частот 3кГц…1МГц (п. 1.2). Дискретная модель такой шумовой помехи с ограниченным энергетическим спектром определяться массивом случайных величин, представляющих ее дискретные отсчеты через интервалы , где - частота дискретизации. Между дискретными отсчетами случайного процесса полностью отсутствуют корреляционные связи. Модель доплеровского сигнала должна корректно учитывать вероятностные и автокорреляционные характеристики сигнала шума.

Образцовые шумовые генераторы (Г2-59, Г2-27), использующие нагретый до проволочный резистор, излучают шум в диапазоне

с неравномерностью СПМ - .

Для генерации «белого» шума на более низких частотах применяется метод гетеродинирования. Дополнительное усложнение структурной схемы генератора шума и увеличение неравномерности спектральной характеристики.

В таблице 2.1 перечислены типовые источники дробового шума тока , где q — заряд электрона; - постоянная составляющая установившегося тока.

Таблица 2.1 – Характеристики источников дробового шума

Источник дробового шума	Частотный диапазон	Неравномерность СПМ, %	Наименование ШГ, где источник применяется
Вакуумные диоды 2Д2С, 2Д3Б	100Гц…100МГц	26…33	Г2-12, Г2-32
p-n переходы электронных элементов [51, 52]	20Гц…10МГц	>10	-
Фотоэлектронный умножитель [50, 51, 54, 55]	50Гц…6МГц	26	Г2-1
Тиратрон	10Гц…5МГц	27	-
Газоразрядные шумовые трубки ГШ-1, ГШ-2 ... ГШ-11	500МГц…4.5ГГц	26…35	СВЧ ШГ

В образцовых генераторах шума необходимо поддерживать температуру с погрешностью менее .

В таблице 2.2 указаны достоинства и недостатки способов генерирования шума с использованием массивов псевдослучайных последовательностей (ПСП) отсчетов [0,0]. В таких последовательностях достигается минимальное присутствие корреляционных связей между элементами.

Таблица 2.2 - Сравнительная оценка методов генерирования ПСП

Метод	Достоинства	Недостатки
Датчиков	Запас чисел не ограничен. Сверхбыстрое получение.	Нестабильность. Невозможность повторения последовательности. Необходимость спец. аппаратуры
Программный	Проверка однократная. Возможность воспроизведения чисел. Простота реализации Отсутствие специальной аппаратуры	Запас чисел ограничен (периодичность). Сравнительно малое быстродействие.
Табличный	Высокое быстродействие. Хорошая случайность. Возможность воспроизведения чисел.	Запас чисел ограничен. Большой объем занимаемой памяти.
Программно-аппаратный	Высокое быстродействие. Возможность воспроизведения чисел.	Запас чисел ограничен. Требуется специальный процессор.

Из таблицы 2.2 видно, что программный метод генерирования ПСП самый удобный с практической точки зрения. Современные ЭВМ в математическом обеспечении имеют встроенную функцию генерирования ПСП с равномерным законом распределения, используя которую можно решать большинство задач моделирования. Предназначенные, как правило, для задач быстрого генерирования ПСП в таких генераторах отсутствуют методы оценки их качества. Исследования вероятностных и корреляционных характеристик таких генераторов, показывают возможные неудовлетворительные результаты.

В разработанной модели генератора шумовой помехи использованы следующие способы воспроизведения ПСП [11]:

линейная конгруэнтная последовательность;
последовательность чисел Фибоначчи с запаздываниями;
библиотечный модуль пакета С++;
последовательность чисел на выходе двоичного сдвигового регистра с обратными связями;
перемешивание последовательностей.

2.2.1 Линейная конгруэнтная последовательность

В настоящее время наиболее популярными генераторами случайных чисел являются генераторы, в которых используется следующий алгоритм, предложенный Д.Г. Лехмером.

, (2.5)

где: a – множитель; с – приращение; m – модуль; X₀ – начальное значение.

Эта последовательность называется линейной конгруэнтной последовательностью. Выбор коэффициентов последовательности определяет ее вероятностные качества. Это можно пояснить следующими рассуждениями.

Вполне очевидно, что конгруэнтная последовательность всегда образует петли, то есть обязательно существует цикл, повторяющийся бесконечное число раз. Это свойство является общим для всех последовательностей вида , где преобразует конечное множество само в себя. Повторяющиеся циклы определяют период последовательности. Длина периода – это одно из требований к линейным конгруэнтным последовательностям. Чтобы обеспечить максимально возможный период повторения конгруэнтной последовательности, представленной (2.5), необходимо выполнить требования ниже приведенной теоремы.

Теорема. Линейная конгруэнтная последовательность, определяемая числами a, с, m и X₀, имеет период m тогда и только тогда когда:

1) числа с и m взаимно простые;

2) b= a-1 кратно p для каждого простого p, являющегося делителем m;

3) b кратно 4, если m кратно 4;

Таким образом, из теоремы следует, что, для того чтобы обеспечить большую длину периода данной последовательности, достаточно выбирать соответственно большое значение модуля m. Однако, процедура нахождения остатка от деления – сравнительно медленно протекающая операция. Этот недостаток можно компенсировать, если значение m выбирать соответствующим длине компьютерного слова.

В представленной программе используется фиксированное значение модуля . Использование такого значения модуля продиктовано следующими обстоятельствами. Во-первых, значение соответствует длине компьютерного слова современных микропроцессоров, используемых в системах ДС. Во-вторых, значение модуля с добавленной единицей увеличивает случайность младших значащих разрядов. При этом операция вычисления остатка от деления по модулю находится как разность между старшими и младшими разрядами. Ниже приведен фрагмент программы вычисления этого остатка.

Листинг 1. Вычисление остатка от деления по модулю

buf=(__int64)a*Number0+c ;

q=buf>>32 ;

r=buf&4294967295 ;

Number0=r-q ;

if (r<q) ;

Number0=Number0+1 ;

Увеличить случайный характер ПСП можно, используя при этом для генерации шума в качестве последовательной выборки только каждый j-ый элемент генерируемой последовательности чисел конгруэнтной последовательности. Поэтому в программе используется интервал сохранения (рисунок 1), при котором в массиве будут сохраняться только значения, соответствующие опции «Интервал сохранения».

2.2.2 Генерация ПСП библиотечной функцией

Данный способ генерации ПСП основан на использовании встроенной (библиотечной) функции _lrand(), вызываемой из файла stdlib.h пакета С++. По качеству случайного процесса этот метод является посредственным, хотя по автокорреляционным характеристикам бывают удачные реализации.

2.2.3 Генерация ПСП на основе последовательности Фибоначчи с запаздыванием.

Метод позволяет увеличить период зацикливания последовательности. Это становится возможным за счет использования последовательности, в которой зависит более чем от одного из предыдущих значений, в результате может быть сформирована последовательность чисел Фибоначчи. В источнике [0] показывается, что последовательность чисел, генерируемая формулой (2.6), имеет период, определяемый выражением :

, (2.6)

где: - задержки (смещения) последовательности;

- модуль.

Как и в линейном конгруэнтном методе, модуль m выбирают равный длине компьютерного слова. При этом задержки, приводящие к длинным периодам, выбирают из таблицы 3.3 [11].

Таблица 2.3 – Задержки, приводящие к длинным периодам по модулю m

24,55	37,100	83,258	273,607	576,3217	7083,19937
38,89	30,127	107,378	1029,2281	4187,9689	9739,23209

Из алгоритма (2.6) генерируемой последовательности можно заметить, что необходима начальная последовательность, из которой формируются задержки. Начальные значения последовательности генерируются с помощью метода линейной конгруэнтной последовательности. Возможно, также пропускать «первые» значения, как рекомендует источник [11].

2.2.4 Генерация ПСП на основе регистра сдвига с обратными связями.

При применении этого метода ПСП получают с помощью генераторов, использующих в качестве основных элементов N-каскадные регистры сдвига и сумматоры по модулю 2. Генератор состоит из стандартных импульсных элементов или их программных реализаций и обеспечивает получение последовательности с максимальным периодом (М-последовательность). Функциональный аналог, использующий данный метод, с одной отрицательной связью, приведен на рисунке 2.4.

Рисунок 2.4 – Схема генератора ПСП на основе сдвигового регистра

Выбор номеров разрядов для подключения обратной связи (ОС) представляет собой непростую задачу, но существуют справочные таблицы, в которых они приведены. В любом случае одна из точек подключения — выход старшего разряда. В таблице 2.4 приведены точки подключения обратной связи для регистров сдвига с разным количеством разрядов N (номера разрядов считаются от нуля).

Таблица 2.4 - Точки подключения обратной связи

число регистров,

номер М регистра для ОС

5, 6

2,4,6,7

13, 14

10,12,13, 15

16,21,22,23

17, 30

Период выходной последовательности генератора составляет (2N - 1) тактов, где N — количество разрядов регистра сдвига. За это время каждое из возможных значений выходного кода (кроме одного) встречается один раз. Количество единиц в выходном сигнале больше количества нулей на единицу.

Более эффективный способ (Фильтр Хаффмана), реализованный как программный продукт, представлен схемой N-разрядного регистра сдвига, выходные сигналы которого после специальной логической обработки снова вводятся в регистр, замыкая тем самым цепь рециркуляции (рисунок 2.5). Этот регистр является базой для построения более совершенного генератора ПСП. При реализации генератора ПСП необходимо выполнение следующих условий:

должно быть задано правило подключения сумматоров по mod2 ключами (коммутаторами) a₁, a₂, ... , a_N (a₀ и a_N всегда равны логической «1»);
из всех ключей a_i , iÎ[1,2,..,N-1] хотя бы одно должно иметь значение «1».

Рисунок 2.5 – Фильтр Хаффмана

Циклические свойства этого генератора ПСП определяются характеристическим многочленом:

где a₀=a_N=1, a_jÎ{0,1}, j=1,2,..N-1. Период последовательности будет максимальным (Т=2^N-1) в том случае, когда многочлен j(x) удовлетворяет условиям примитивности и неприводимости. В нахождении такого многочлена заключается основная задача синтеза генератора псевдослучайных последовательностей максимальной длины. При этом на выходе данного генератора получаются равномерно распределенные псевдослучайные числа.

2.2.5. Анализ алгоритмов ПСП, не включенных в модель доплеровского сигнала.

1) Алгоритм Блюма-Блюма-Шуба.

В 1986 году Ленор Блюм, Мануэль Блюм и Майкл Шуб предложили алгоритм генерации псевдослучайной последовательности, стойкий к обратным преобразованиям. Основная рекуррентная формула алгоритма:

x_n = (x_n₋₁)² mod pq, z_n = parity (x_n),

где p и q — два больших простых числа.

Для повышения качества получаемой последовательности на очередном шаге выбираются не все биты x_n, а только младшие, или даже только бит четности. Из полученных «случайных битов» формируются двоичные псевдослучайные числа произвольной разрядности. Одной из особенностей вычислительной формулы является сквозная возможность вычислить x_n без генерации всех предыдущих членов последовательности:

x_n = (x₀)^{2n mod (p − 1)(q − 1)} mod pq,

Данный алгоритм более требователен к вычислительным ресурсам, но, с другой стороны, обладает хорошими статистическими характеристиками.

2) Алгоритм xor-shift.

Профессором университета Флориды Джорджем Марсаглией был разработан очень быстрый генератор, который был назван «xor-shift». «Псевдокод» на Турбо Паскале выглядит следующим образом:

Листинг 2.var x : LongWord = 3456789; y : LongWord = 62436069, z : LongWord = 1288629, w : LongWord = 675123;function xor128: LongWord;var t : LongWord;begin t := (x xor (x shl 11)); x := y; y := z; z := w; xor128 := w = (w xor (w shr 19)) xor (t xor (t shr 8)));end;

Комбинация данного алгоритма с линейным конгруэнтным алгоритмом и алгоритмом Фибоначчи с запаздываниями представлена ниже.

Листинг 3.

program Sample;var x : LongWord = 123456789; y : LongWord = 362436000; z : LongWord = 521288629; c : LongWord = 7654321; function Random() : LongWord;var t : int64;begin x := int64(69069)*x + 12345; y := y xor (y shl 13); y := y xor (y shr 17); y := y xor (y shl 5); t := int64(698769069)*z + c; c := t shr 32; z := t; Random := x + y + z;end; begin {...} writeln ( Random() );end.

Данные алгоритмы не были включены в модель доплеровского сигнала по причине сложности эксплуатации первого и примитивности (с недостаточно качественными статистическими характеристиками ПСП) второго.

2.2.6 Метод перемешивания.

Чтобы получить наиболее оптимальный вариант шумовой помехи близкий к белому шуму в способе воспроизведения используется перемешивание ПСП. Метод перемешивания считается прекрасным средством уменьшения корреляционной зависимости генерируемых последовательностей.

В модели генератора шумовой помехи реализован следующий способ. Воспроизводится дополнительная ПСП, которая определяет позицию перемешиваемых чисел в исходной последовательности. В соответствии со своими позициями числа исходной последовательности перестанавливаются. При этом задается буфер, в пределах которого происходит перемешивание, а также предусмотренная возможность зациклить метод n-ое число раз.

Однако методы перемешивания имеют «врожденный дефект». Они изменяют порядок следования генерируемых чисел, но не сами числа. В большинстве случаев порядок следования является решающим фактором. Если генератор случайных чисел не удовлетворяет критериям «Монобитный тест» или «Тест длинные цепочки» (см. ниже), то положение после перемешивания может не улучшиться. Для этого в способе предусмотрена операция циклического сдвига содержимого ячейки влево и вправо, реализация которой состоит в следующем. В ячейке хранится начальное число . Циклически сдвигая содержимое ячейки влево на 2 разряда длины ячейки, получаем новое число . Точно так же, циклически сдвигая содержимое ячейки вправо на 2 разряда длины ячейки, получаем второе число . Сумма чисел и дает новое случайное число. Кроме того, для дополнительного увеличения случайности воспроизводимых ПСП в качестве последовательной выборки используется только каждый j-ый элемент генерируемой последовательности, как рекомендует источник [11].

2.3 Статистические тесты на случайность

Естественно, что все эти способы имеют свои достоинства и недостатки с точки зрения эффективности генерации квазибелого шума, что, в свою очередь, требует сравнительного анализа качества генерируемых ПСП. Для оценки качества ПСП важнейшее значение имеет теоретическое определение статистических характеристик и корреляционных связей [8]. На основе анализа существующих методов оценки статистических и корреляционных характеристик ПСП были выбраны пять алгоритмов тестов, рекомендованных стандартом FIPS 140 национального института стандартов США [28]. Все тесты являются бинарными тестами. Это связано с простотой их реализации и быстротой их вычисления. Тесты реализуются над массивами ПСП длиной по бит. Для этого исходная последовательность ПСП разбивается на массивы размером бит. В случае удовлетворительного прохождения тестов каждой под последовательностью, в целом, тест считается пройденным. Также эти тесты для ПСП являются вероятностными. Это значит, что результат теста звучит, как "эта ПСП подходит" или "эта ПСП с вероятностью ошибки не более не подходит". Это вполне естественно, так как любой тест может проверить лишь последовательность битов конечной длины, которая случайно может оказаться неприемлемой. Основным параметром всех тестов является - вероятность того, что тест забракует хороший генератор. Стандарт FIPS 140 устанавливает на уровне 0.01. Статистические тесты на случайность рекомендованные стандартом FIPS 140 приводятся ниже.

2.3.1 Монобитный тест.

Тест основан на равенстве частот повторения логических «1» и «0» в идеальной ПСП. В тесте вычисляется значение:

, (2.7)

где: - число битов в проверяемой последовательности;

- число 1; - число 0.

Если значение превысит некоторый порог (который зависит от ), то генератор не проходит тест. Поскольку имеет приблизительно распределение с одной степенью свободы, то в качестве порога используется число 6,6 (рекомендуется стандартом FIPS 140).

Единственной сложностью здесь является эффективный подсчет числа различных битов, так как в большинстве современных вычислительных архитектур нет команд для работы с отдельными битами. Для подсчета количества единичных битов использован метод, описанный в. Число мысленно разбивается на ячейки, равной длины и биты в старшей и младшей половинах ячейки рассматривается как число битов в соответствующей части ячейки. Затем параллельно для всех ячеек число битов в обеих половинах ячейки суммируются, и результат записывается в младшую часть. Вначале суммирование производится для ячеек размером 2 бита, потом 4 и так далее до 32. В результате мы получаем полное число битов за логарифмическое (от длины машинного слова) время. Далее представлена несколько оптимизированная реализация этого алгоритма на языке С++:

Листинг 4. Подсчет единичных битов в числе

inline int countBits( uint x )

{

x = x - ((x >> 1) & 0x55555555); // 2- битовые ячейки

x = (x & 0x33333333) + ((x >> 2) & 0x33333333); // 4- битовые ячейки

x = (x + (x >> 4)) & 0x0F0F0F0F; // 8- битовые ячейки

x = x + (x >> 8); // 16- битовые ячейки

x = x + (x >> 16); // 32- битовые ячейки

x = x & 0x3F; // Обнуляем старшие разряды содержащие «мусор»

return x;

}

После этого реализация самого теста достаточно проста. В дальнейшем будет приводиться не весь текст функции теста, а только основная его часть.

Листинг 5. Реализация монобитного теста

inline double monobitTest(int address,int sequenceLength)

{

int n1 = 0, n0 = 0;

double X1;

for ( int i = 0; i < sequenceLength; i++ )

n1 += countBits(*(Data+address+i));

n0 = INT_BITS * sequenceLength - n1;

X1 = ((double)n1 - n0)*((double)n1 - n0) / ((double)INT_BITS * sequenceLength);

if( X1 > 6.63 ) // Порог

res = false; // Тест не пройден

else

res = true; // Тест пройден

} // monobitTest

2.3.2 Покер-тест

В тесте последовательность разбивается на блоки длиной т бит. Тест основан на том, что в идеальной случайной последовательности вероятность всех блоков одинакова. В покерном тесте вычисляется статистика:

, (2.8)

где: - суммарное число т - битных блоков в исследуемой последовательности;

- число т - битных блоков, двоичное представление числа i.

Стандарт FIPS 140-1 устанавливает т = 4 и = 20000 бит. Поскольку Х₂ имеет распределение со степенями свободы, то для т = 4 выбран порог равный 30,6 (рекомендуется стандартом FIPS 140).

Эффективный алгоритм подсчета встречаемости различных блоков основан на использовании таблицы (использование таблиц может быть целесообразно лишь при небольшом размере блоков, то есть при 4т16 в зависимости от приложения).

Листинг 6. Подсчет встречаемости m-битных блоков

inline double pokerTest( int address,int sequenceLength)

{

const int blockNum = 1 << POKER_BLOCK_LEN;

const unsigned int blockMask = blockNum - 1;

unsigned int x;

int blockCounter[blockNum] = {0};

double X2 = 0;

for( int i = 0; i < sequenceLength; i++ )

{

x=*(Data+address+i);

for( unsigned int j = 0; j < INT_BITS / POKER_BLOCK_LEN; j++ )

{

blockCounter[ x & blockMask ]++;

x = x >> POKER_BLOCK_LEN;

}

for( int i = 0; i < blockNum; i++ )

X2 += blockCounter[i] * blockCounter[i];

X2 = X2 * blockNum * POKER_BLOCK_LEN / (INT_BITS * sequenceLength)

- (double)(INT_BITS * sequenceLength) / POKER_BLOCK_LEN;

return X2;

}

2.3.3 Серийный тест.

В тесте определяется число вхождений серий одинаковых битов различной длины. Тест основан на том, что в идеальной случайной последовательности среднее число серий длиной равно .

В тесте вычисляется статистика:

, (2.9)

где: , - число единичных (нулевых) серий в послед. длиной ;

Поскольку Х₃ имеет распределение с 2п-2 степенями свободы. Для = 20000 бит, п=9 имеем порог равный 32,0 (рекомендуется стандартом FIPS 140).

Алгоритм вычисления длины битовых блоков основан на том, что число содержит п единичных битов. Для произвольного числа x, содержащего серию нулевых битов длиной п в младших разрядах, содержит серию из п + 1 единичных битов в младших разрядах (все остальные биты нулевые). Длину выделенной таким образом канонической серии единичных битов можно считать бинарным поиском [11], либо с помощью заранее вычисленной таблицы (если длина серии мала). В программе использован более эффективный комбинированный метод:

Листинг 7. Подсчет длинны серии нулевых битов в младших разрядах

inline int runLength( unsigned int x )

{

int length = 0; // Длина серии

unsigned int y; // Приводим x к каноническому виду

x = (x ^ (x-1)) >> 1; //Считаем длину серии единичных битов с точностью до 8:

y = x >> 16; if( y ) { length += 16; x = y; }

y = x >> 8; if( y )

{ length += 8; x = y; } //Уточняем длину с помощью таблицы:

return length + smallRunLength[x];

}

Таблица smallRunLength содержит длины серий единичных битов для чисел от 0 до 255. Заметим, что можно было бы использовать алгоритм подсчета единичных битов, однако, проведенное исследование показало, что он в данном случае менее эффективен, так как не учитывает комбинацию, когда все единичные биты прижаты к правому краю. Поскольку ПСП генерируемых чисел рассматривается, как последовательность бит, то необходимо учитывать, что серия битов может быть разорвана (лежать на границе двух чисел). Программа подсчета различных серий, учитывает последнее замечание.

2.3.4 Тест «Длинные цепочки».

Тест проверяет наличие одинаковых цепочек, длинна которых, превышает 33 бита («явная» автокорреляция). Присутствие таких цепочек в последовательности служит признаком не случайности ПСП.

2.3.5 Автокорреляционный тест.

Тест основан на том, что в идеальной случайной последовательности нет (либо крайне мало) повторяющихся подпоследовательностей. В тесте подсчитывается число совпадающих битов в исходной и сдвинутой на бит последовательностях. Статистика вычисляется как:

, (2.10)

где: – i-й бит последовательности.

Поскольку Х₅ имеет нормальное распределение с нулевым средним и дисперсией равной 1, то порог равен 2.33 (рекомендуется стандартом FIPS 140).

Листинг 8. Вычисление функции автокорреляции

inline double autocorTest( int address,int sequenceLength)

{

unsigned int x, next, shifted;

int autoCor = 0;

double X5 = 0;

x=*(Data+address);

for ( int i = 1; i < sequenceLength; i++ )

{

next =*(Data+address+i);

shifted = (next << (INT_BITS - AUTOCOR_SHIFT_SIZE))

| (x >> AUTOCOR_SHIFT_SIZE);

autoCor += countBits( x ^ shifted );

x = next;

}

X5 = (2.0 * autoCor - INT_BITS * sequenceLength + AUTOCOR_SHIFT_SIZE)

/ sqrt( INT_BITS * sequenceLength - AUTOCOR_SHIFT_SIZE );

X5 = fabs( X5 );

return X5;

}

В итоге сгенерированная ПСП любым из методов считается случайной, если она удовлетворяет всем пяти статистическим тестам (2.7) - (2.10) стандарта FIPS 140.

Для представления ПСП в виде сигнала шумовой помехи сгенерированная последовательность, удовлетворившая критериям стандарта FIPS 140, масштабируется в интервал значений -0,5..0,5.

2.4 Модель дискретного доплеровского сигнала

Дискретная модель доплеровского колебания при отсутствии шумовой помехи и затухания сигнала с учетом (2.3), (2.4) формируется как:

,, (2.11)

где: – период дискретизации, связанный с частотой дискретизации F в канале обработки сигнала выражением F=1/Т;

i – номер выборки, i = 1, 2, 3, ... , N (N – количество выборок);

Длительность интервала воспроизведения определяется выражением .

В модели воспроизводимого доплеровского сигнала затухание уровня доплеровского колебания с увеличением расстояния от антенн ДИИС до ЛО малых размеров с учетом динамики соотношения С/Ш изменяется согласно (2.4). Шум – процесс стационарный, следовательно, значение его дисперсии остаётся независимым от времени. Таким образом, для установки уровня шума относительно уровня сигнала введём масштабирующий коэффициент . Для определения уровня сигнала относительно уровня шума в конце наблюдаемого интервала времени (i=N) введён коэффициент масштаба , при котором выполняется (2.4). В начальный момент, когда i=1, выполняется: , откуда следует, что:

, (2.12) .

В результате с учетом выражений (2.11), (2.12) суммарный (зашумленный) дискретизированный доплеровский сигнал с учетом затухания уровня колебания по мере удаления ЛО малых размеров от антенн ДИИС будет определяться выражением:

(2.13)

где - дискретные отсчеты модели шумовой помехи.

Коэффициенты n1 и n2 рассчитываются по формулам:

, ,

где: – отношение сигнал/шум (С/Ш) в начале полета, дБ;

- отношение шум/сигнал (Ш/С) в конце полета, дБ.

Дискретная модель зашумленного доплеровского сигнала на выходе модуля АРУ масштабируется коэффициентом усиления . Коэффициент усиления определяется для каждого отсчета согласно формуле [96]:

, (2.14)

где: - квадрат эффективного значения порога АРУ,

- количество отсчетов;

- постоянная времени фильтров реальных АРУ.

Таким образом, квадрат эффективного значения дискретного зашумленного доплеровского сигнала остается постоянным и соответствует значению . Регулируя значение доплеровский сигнал можно вписывать в требуемый диапазон уровней. Постоянная времени соответствует постоянной времени фильтров реальных модулей АРУ в аттестуемых системах ДИИС.

Согласно соотношениям (2.13), (2.14) воспроизводится дискретная модель зашумленного доплеровского сигнала, соответствующая реальным сигналам, полученным для удаляющихся по инерции ЛО малых размеров на конечном интервале времени, получивших положительное ускорение в первый момент времени полета. Воспроизводимые модели предназначены для аттестации средств распознавания и измерения параметров доплеровских сигналов.

На основе выше изложенного материала разработан программный модуль Doppler_Project.exe, позволяющий воспроизводить массив дискретного зашумленного доплеровского сигнала. Программный модуль написан на языке программирования C++ в среде программирования C++ Builder 6.0 [2]. Программный код программного модуля представлен в приложении А.

3 Экспериментальные исследования

Задачей данного раздела является исследование эффективности разработанных программных средств, реализующих разработанный способ воспроизведения зашумленных быстроубывающих доплеровских сигналов.

3.1 Модель шумовой помехи

Проведены экспериментальные испытания воспроизведения элементов шумовой помехи . Параметры методов воспроизведения:

линейный конгруэнтный (ЛК):, , , ;
последовательность Фибоначчи с запаздываниями (Ф): (83;258);
библиотечный модуль пакета C++ (Б);
сдвиговый регистр с обратными связями (СР): полином 79764919;
метод перемешивания (МП): размер буфера 300 элементов.

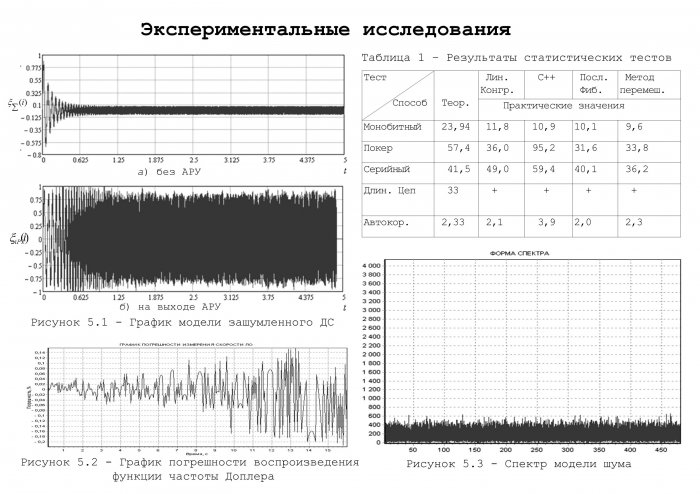
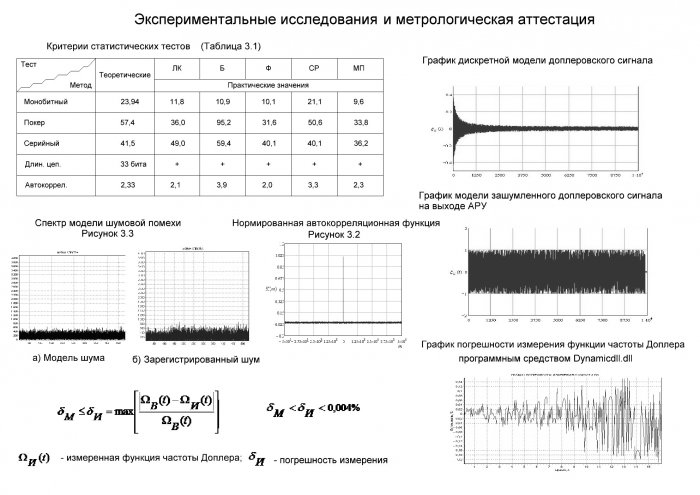
Статистические и корреляционные характеристики ПСП оценены пятью тестами стандарта FIPS 140. В таблице №4 представлены результаты тестов.

Таблица 3.1 - Критерии статистических тестов

Тест Метод	Теоретические	ЛК	Б	Ф	СР	МП
Тест Метод	Теоретические	Практические значения
Монобитный	23,94	11,8	10,9	10,1	21,1	9,6
Покер	57,4	36,0	95,2	31,6	50,6	33,8
Серийный	41,5	49,0	59,4	40,1	40,1	36,2
Длин. цеп.	33 бита	+	+	+	+	+
Автокоррел.	2,33	2,1	3,9	2,0	3,3	2,3

Согласно таблице 3.1, реализации: метод генерирования ПСП с использованием линейного конгруэнтного метода, библиотечной функции, метода сдвигового регистра с обратными связями по разным тестам не удовлетворили требованию стандарта FIPS-140. Использование метода перемешивания для этих последовательностей позволяет повысить случайность, и тем самым удовлетворить критериям стандарта.

Оценены вероятностные и спектрально-корреляционные характеристики процесса генерированного методом - последовательность чисел Фибоначчи с запаздываниями (Ф).

Математическое ожидание для реализаций процесса:

, (3.1)

, ,

, .

Дисперсия процесса [3]:

, (3.2)

Изменение математического ожидания (3.1) и среднеквадратического отклонения (3.2) процесса составляет менее 1%. Процесс - стационарным.

График реализации процесса шумовой помехи и его визуальный вид изображен на рисунке 3.1.

а) график модели б) визуальный вид

Рисунок 3.1 –Модель шумовой помехи

Оценкой качества такой последовательности считается то, что массив точек ПСП равномерно распределяется по всей канве, и отсутствуют явно выраженные визуальные сгустки.

Оценкой качества корреляционных свойств процесса служит максимальное отклонение модуля нормированной автокорреляционной функции процесса от дельта–функции.

где - смещение процесса .

На рисунке 3.2 изображена нормированная автокорреляционная функции для реализации процесса .

Рисунок 3.2 - Нормированная автокорреляционная функция

Спектр шумовой помехи изображен на рисунке 3.3. По форме спектр имеет равномерный характер без ярко выраженных спектральных всплесков (отсутствуют корреляционные связи).

а) Модель шума б) Зарегистрированный шум

Рисунок 3.3 - Спектр модели шумовой помехи

В результате сделан вывод, что по статистические и корреляционные характеристики модели шумовой помехи приближены к характеристикам белого шума.

3.2 Метрологическая аттестация моделей доплеровского сигнала

На рисунке 3.4 изображен график дискретной модели зашумленного доплеровского сигнала для дБ и дБ.

Рисунок 3.4 - График дискретной модели доплеровского сигнала

На рисунке 3.5 изображен график дискретной модели зашумленного доплеровского сигнала на выходе модуля АРУ.

Рисунок 3.5 - График модели зашумленного доплеровского сигнала

на выходе АРУ

Модель доплеровского сигнала, воспроизводимая программой Doppler_Project.exe, в первую очередь, предназначена для аттестации методов обработки зашумленных доплеровских сигналов по разрешающей способности распознавания и точности измерения мгновенных значений частоты Доплера. Для исследования точности воспроизведения самой модели оценивается погрешность воспроизведения детерминированной функции частоты Доплера (2.3) посредством ее измерения:

, (3.3)

где: - измеренная функция частоты Доплера;

- погрешность измерения.

В погрешность измерения входят составляющие погрешностей, как средства воспроизведения , так и средства измерения . Разумеется, что средство измерения частоты Доплера, предназначенное для аттестации модели должно обладать приемлемой точностью: .

В качестве средства измерения для метрологической аттестации модели использовалась программное средство Dynamicdll.dll с функцией Method_ STT_AN (TSTT *P_stt).

Рисунок 3.6 – График погрешности измерения функции частоты Доплера программным средством Dynamicdll.dll

На основании ряда экспериментальных измерений моделей доплеровского колебания установлено, что максимальная погрешность измерения функции частоты Доплера удовлетворяет неравенству: . Поскольку в обозначенную погрешность входят составляющие погрешности как средства воспроизведения (Doppler_Project.exe) , так и погрешность средства измерения частоты Доплера (функция Method_ STT_AN (TSTT *P_stt)), то можно утверждать, что погрешность воспроизведения модели доплеровского колебания не превышает оцененной максимальной погрешности измерения .

Таким образом, аттестованные модели доплеровского колебания можно использовать как меру, имеющую погрешность воспроизведения функции частоты Доплера .

4 Экономический расчет

Расчет затрат на разработку программного обеспечения.

Расчет на стадии разработки устройства

Создание устройства связано с проведением опытно-конструкторских работ, стоимость которых определяется следующим образом:

(1),

где:

– стоимость проведения эскизно-технического проектирования и разработки конструкторской документации, руб.;

–0 стоимость разработки программного обеспечения, руб.;

– стоимость изготовления опытного образца с учетом отладки, руб.

Стоимость проведения эскизно-технического проектирования и разработки конструкторской документации включает затраты на оплату труда разработчиков, накладные расходы и контрагентские расходы.

Затраты на оплату труда разработчиков включают основную и дополнительную заработную плату, а также отчисления на социальные нужды, которые рассчитываются по формуле:

(2),

где:

t – трудоемкость проведения эскизно-технического проектирования и разработки конструкторской документации, часов;

– оклад инженера-разработчика за месяц, руб./мес.;

– фонд рабочего времени работника за месяц, ч./мес.;

– процент премии, % (25-30%);

– районный коэффициент, % (15%).

Фонд рабочего времени работника определяется по формуле

(3),

где:

– количество рабочих дней в месяце, дней (21-26 день)

– продолжительность рабочего дня, ч (8-6 часов);

дней

тогда по формуле (2): руб.

Дополнительная заработная плата разработчика определяется по формуле:

(4),

где:

– норматив дополнительной заработной платы, % (15-20%);

руб.

Отчисления на социальные нужды рассчитываются следующим образом:

(5),

где:

– норматив отчислений на социальные нужды, % (34,2%).

руб.

Таким образом затраты на заработную плату составят:

(6),

руб.

Накладные расходы определяются пропорционально основной заработной плате по формуле:

(7),

где:

– норматив накладных расходов, % (20-60%),

руб.

В результате стоимость проведения эскизно-технического проектирования и разработки конструкторской документации составит:

(8),

руб.

Стоимость разработки программного обеспечения включает затраты на вспомогательные (расходные) материалы (бумага, дискеты), затраты на оплату труда программиста, затраты на оплату машинного времени и накладные расходы.

Затраты на вспомогательные материалы в данной работе не учитываются из-за незначительной величины.

Затраты на оплату труда программиста определяются по формулам (2)–(6) при условии, что

t – трудоемкость разработки программного обеспечения, ч.;

– оклад программиста за месяц, руб./мес.;

руб.;

руб.

Затраты на оплату машинного времени определяются по формуле:

(9),

руб.

где:

– трудоемкость отладки и оформления документации на компьютере, ч. (50-70% от трудоемкости разработки программного обеспечения);

– стоимость машино-часа работы ЭВМ, руб./час;

(10),

руб./час,

где:

– полные затраты на эксплуатацию ЭВМ в течение года, руб./год;

–действительный годовой фонд работы ЭВМ, ч./год;

(11),

где:

– количество рабочих дней в году (260-320 дней);

– длительность рабочего дня (6-8 часов);

– количество смен (1-2 смена);

– процент потерь рабочего времени на ремонтно-профилактические работы, % (3-5%);

ч./год.

Полные затраты на эксплуатацию ЭВМ определяются по формуле:

(12),

руб./год.

где:

– годовые издержки на зарплату обслуживающего персонала;

– годовые издержки на амортизацию;

– годовые издержки на электроэнергию потребляемую ЭВМ;

– годовые издержки на расходные материалы;

– годовые издержки на текущее техническое обслуживание и ремонт ЭВМ;

– прочие расходы;

(13),

где:

– оклад i-той категории обслуживающего персонала, руб./мес.;

– численность i-той категории обслуживающего персонала, чел;

– количество ЭВМ (10-15 шт.);

В данной работе принимаем, что обслуживанием ЭВМ занимается один работник, 1500–2000 р./мес., тогда:

руб./год;

Годовые издержки на амортизацию:

(14),

где:

– балансовая стоимость ЭВМ (30000 руб.);

– норма амортизации;

(15),

где:

– срок полезного использования (3-5 года).

Тогда по формулам (14) и (15):

руб.

Годовые издержки на электроэнергию потребляемую ЭВМ определяются по формуле:

(16),

где:

– суммарная мощность ПК (0,25-0,3 кВт);

– тариф на электроэнергию (2,86 руб./кВт);

– коэффициент использования мощности (0,9);

руб.

Годовые издержки на текущее техническое обслуживание и ремонт ЭВМ определяются по формуле:

(17),

где:

– норматив затрат на текущее техническое обслуживание и ремонт, % (3-5%);

руб.

Годовые издержки на расходные материалы определяются по формуле:

(18),

где:

– коэффициент затрат на вспомогательные расходные материалы, % (0,8-1%);

руб.

Прочие расходы определяются по формуле:

(19),

где:

– коэффициент прочих расходов, % (5-7%);

руб.

Накладные расходы, включаемые в стоимость разработки программного обеспечения определяются по формуле (7), из основной заработной платы программиста:

руб.

Таким образом, стоимость разработки программного обеспечения составит:

(20),

руб.

В итоге затраты на данное программное обеспечение составят:

6151,85- стоимость разработки программного обеспечения

Таблица – Расчет программного обеспечения.

Наименование	Ед. измерения	Значения
Затраты на оплату труда программиста	руб.	5355,9
Затраты на оплату машинного времени	руб.	101,85
Накладные расходы	руб.	694,1
Итого:	руб.	6151,85

5 Безопасность труда

5.1 Анализ и обеспечение безопасных условий труда.

Принцип нормирования микроклимата – создание оптимальных условий для теплообмена тела человека с окружающей средой.

Объем помещений, в которых размещены работники вычислительных центров, не должен быть меньше 19,5м3/человека у учетом максимального числа одновременно работающих в смену. Нормы подачи свежего воздуха в помещения, где расположены компьютеры, приведены в табл. 5.2.

Таблица 5.1 – Параметры микроклимата для помещений, где установлены компьютеры.

Период года	Параметр микроклимата	Величина
Холодный	Температура воздуха в помещении	22…24̊ С
	Относительная влажность	40…60%
	Скорость движения воздуха	до 0,1м/с
Теплый	Температура воздуха в помещении	23…25 ̊С
	Относительная влажность	40…60%
	Скорость движения воздуха	0,1…0,2м/с

Таблица 5.2 – Нормы подачи свежего воздуха в помещения, где расположены компьютеры.

Характеристика помещения		Объемный расход подаваемого в помещение свежего воздуха, м3/ на одного человека в час
Объем	до 20м3 на человека	Не менее 30
	20…40м3 на человека	Не менее 30
	более 40м3 на человека	Естественная вентиляция

Для обеспечения комфортных условий используются как организационные методы (рациональная организация проведения работ в зависимости от времени года и суток, чередование труда и отдыха), так и технические средства (вентиляция, кондиционирование воздуха, отопительная система).

Шум ухудшает условия труда оказывая вредное действие на организм человека. Длительное воздействие интенсивного шума (выше 80 дБ(А)) на слух человека приводит к его частичной или полной потере.

В табл. 5.3 указаны предельные уровни звука в зависимости от категории тяжести труда, являющиеся безопасными в отношении сохранения здоровья и работоспособности.

Таблица 5.3 – предельные уровни звука, дБ, на рабочих местах.

Категория напряженности труда	Категория тяжести труда
Категория напряженности труда	I.Легкая	II.Средняя	III.Тяжелая	IV.Очень тяжелая
I. Мало напряженный	80	80	75	75
II. Умеренно напряженный	70	70	65	65
III. Напряженный	60	60	-	-
IV. Очень напряженный	50	50	-	-

Уровень шума на рабочем месте не должен превышать 50дБ, а в залах обработки информации на вычислительных машинах – 65дБ. Для снижения уровня шума стены и потолок помещений, где установлены компьютеры, мт облицованы звукопоглощающими материалами. Уровень вибрации в помещениях вычислительных центров может быть снижен путем установки оборудования на специальные виброизоляторы.

Допустимые значения параметров неизолирующих электромагнитных излучений от монитора компьютера представлены в табл. 5.4.

Максимальный уровень рентгеновского излучения на рабочем месте оператора обычно не превышает 10мкбэр/ч, а интенсивность ультрафиолетового и инфракрасного излучений от экрана монитора лежит в пределах 10…100мВт/м2.

Таблица 5.4 – Допустимые значения параметров неионизирующих электромагнитных излучений (в соответствии с СанПиН 2.2.2.542-96)

Наименование параметра	Допустимые значения
Напряженность электрической составляющей электромагнитного поля на расстоянии 50см от поверхности видеомонитора	10В/м
Напряженность магнитной составляющей электромагнитного поля на расстоянии 50см от поверхности видеомонитора	0,3А/м
Напряженность электростатического поля не должна превышать: - для взрослых пользователей - для детей дошкольных учреждений и учащихся - средних специальных и высших учебных заведений	20кВ/м 15кВ/м

Для снижения воздействия этих видов излучения рекомендуется применять мониторы с пониженным уровнем излучения (MPR-II, TCO-92,TCO-99), устанавливать защитные экраны, а также соблюдать регламентированные режимы труда и отдыха.

Проектирование рабочих мест, снабженных видеотерминалами, относится к числу важных проблем эргономического проектирования в области вычислительной техники.

Оптимальное размещение предметов труда и документации в зонах досягаемости представлено на рисунке 5.1.

Рисунок 5.1 – Размещение основных и периферийных составляющих ПК.

сканер, 2- монитор, 3- принтер, 4 – поверхность рабочего стола,

5 – клавиатура, манипулятор типа “мышь”.

Высота рабочей поверхности рекомендуется в пределах 680-760мм.

Высота поверхности, на которую устанавливается клавиатура, должна быть около 650мм.

Рекомендуемая высота сиденья над уровнем пола находится в пределах 420-550мм.

Расстояние от глаз до экрана делают больше (около 700мм), чем расстояние от глаза до документа (300-450мм). Вообще при высоком качестве изображения на видеотерминале расстояние от глаз пользователя до экрана, документа и клавиатуры может быть равным.

Положение экрана определяется:

-расстояние считывания (0,6…0,7);

-углом считывания, направлением взгляда 20̊ ниже горизонтали к центру экрана, причем экран перпендикулярен этому направлению.

Должна также предусматриваться возможность регулирования экрана:

-по высоте +3 см;

-по наклону от -10̊ до +20̊ относительно вертикали;

- в левом и правом направлениях.

Требования к рабочей позе пользователя видеотерминала следующие:

-голова не должна быть наклонена более чем на 20̊ ,

-плечи должны быть расслабленны,

- локти под углом 80̊ …100̊ ,

-предплечья и кисти рук – в горизонтальном положении.

Создание благоприятных условий труда и правильное эстетическое оформление рабочих мест на производстве имеет большое значение как для облегчения труда, так и для повышения его привлекательности, положительно влияющей на производительность труда.

Расчет освещенности рабочего места сводится к выбору системы освещения, определению необходимого числа светильников, их типа и размещения. Исходя из этого, рассчитаем параметры искусственного освещения.

Обычно искусственное освещение выполняется посредством электрических источников света двух видов: ламп накаливания и люминесцентных ламп. Будем использовать люминесцентные лампы, которые по сравнению с лампами накаливания имеют ряд существенных преимуществ:

-по спектральному составу света они близки к дневному, естественному свету;

-обладают более высоким КПД ( в 1,5-2 раза выше, чем КПД ламп накаливания);

-обладают повышенной светоотдачей (в 3-4 раза выше, чем у ламп накаливания);

-более длительный срок службы.

Расчет освещения проводится для комнаты площадью 15м2, ширина которой 5м, высота 3м. воспользуемся методом светового потока.

Для определения количества светильников определим световой поток, падающий на поверхность по формуле:

, где

F – рассчитываемый световой поток, Лм;

E – нормированная минимальная освещенность, Лк (определяется по таблице). Работу программиста, в соответствии с этой таблицей, можно отнести к разряду точных работ, следовательно, минимальная освещенность будет Е=300Лк;

S –площадь освещаемого помещения (в нашем случае S=15м2);

Z – отношение средней освещенности к минимальной (обычно применяется равным 1,1…1,2, пусть Z=1,1);

K – коэффициент запаса, учитывающий уменьшение светового потока лампы в результате загрязнения светильников в процессе эксплуатации (его значение зависит от типа помещения и характера проводимых в нем работ и в нашем случае К=1,5);

n- коэффициент использования, (выражается отношением светового потока, падающего на расчетную поверхность, к суммарному потоку всех ламп и исчисляется в долях единицы; зависит от характеристик светильника, размеров помещения, окраски стен и потолка, характеризуемых коэффициентами отражения от стен (РС) и потолка (РП)), значение коэффициентов РС и РП были указаны выше: РС=40%, РП=60%. Значение n определим по таблице коэффициентов использования различных светильников. Для этого вычислим индекс помещения по формуле:

, где

S – площадь помещения, S=15 м2;

h – расчетная высота подвеса, h=2,92 м;

A – ширина помещения, А=3 м;

B – длина помещения, В=5 м.

Подставив значения получим:

Зная индекс помещения I, находим n=0,22

Подставим все значения в формулу для определения светового потока F:

=33750 Лм.

Для освещения выбираем люминесцентные лампы типа ЛБ40-1, световой поток которых F=4320 Лк.

Рассчитаем необходимое количество ламп по формуле:

, где

N – определяемое число ламп;

F – световой поток, F=33750;

Fл – световой поток лампы, Fл=4320 Лм.

5.2 Расчет мероприятия по улучшению безопасных условий труда.

Одним из неблагоприятных факторов производственной среды в ИВЦ является высокий уровень шума, создаваемый печатными устройствами, оборудованием для кондиционирования воздуха, вентиляторами систем охлаждения в самих ЭВМ.

Для решения вопросов о необходимости и целесообразности снижения шума необходимо знать уровни шума на рабочем месте оператора.

Уровень шума, возникающий от нескольких некогерентных источников, работающих одновременно, подсчитывается на основании принципа энергетического суммирования излучении отдельных источников:

где

Li – уровень звукового давления i-го источника шума;

n – количество источников шума.

Полученные результата расчета сравниваются с допустимым значением уровня шума для данного рабочего места. Если результаты расчета выше допустимого значения уровня шума, то необходимы специальные меры по снижению шума. К ним относятся: облицовка стен и потолка зала звукопоглощающими материалами, снижение шума в источнике, правильная планировка оборудования и рациональная организация рабочего места оператора.

Уровни звукового давления источников шума, действующих на оператора на его рабочем месте представлены в таблице 5.6.

Таблица 5.6 – Уровни звукового давления различных источников.

Источник шума	Уровень шума, дБ
Жесткий диск	40
Вентилятор	45
Монитор	17
Клавиатура	10
Принтер	45

Обычно рабочее место оператора оснащено следующим оборудованием: винчестер в системном блоке, вентилятор(ы) систем охлаждения ПК, монитор, клавиатура, принтер и сканер.

Подставим значения уровня звукового давления для каждого вида оборудования в формулу, получим:

Полученное значение не превышает допустимый уровень шума для рабочего места оператора, равный 65 дБ (ГОСТ 12.1.003-83). И если учесть что такие периферийные устройства как сканер и принтер не будут использоваться одновременно, то это цифра будет еще ниже. Кроме того при работе принтера непосредственное присутствие оператора необязательно, т.к. принтер снабжен механизмом автоподачи листов.

5.3. Возможные чрезвычайные ситуации.

Чрезвычайными ситуациями называют обстоятельства, возникающие в результате стихийных бедствий, аварий и катастроф в промышленности, транспорте, диверсий, экологических катастроф.

Чрезвычайная ситуация – это состояние, при котором на объекте нарушаются нормальные условия жизни и деятельности персонала, возникает угроза жизни и здоровью людей, наносится физический, материальный и моральный ущерб.

Наиболее вероятная чрезвычайная ситуация, которая может произойти в непосредственной близости от административного здания это выброс какого-либо активного химически опасного вещества(АХОВ), например аммиака, в результате аварии.

Аммиак – бесцветный газ с запахом нашатыря (порог всприятия 0,037 мг/л). Сухая смесь аммиака с воздухом (4:3) взрывается. Хорошо растворяется в воде. В высоких концентрациях аммиак возбуждает центральную нервную систему и вызывает судороги, также жидкий аммиак используется как хладагент в холодильных установках. ПДК аммиака в воздухе рабочей зоны составляет 0,02 мг/л.

В легких случаях отравления отмечается раздражение носоглотки и глаз, чиханье сухость и першение в горле, охриплость, кашель и боли в груди. В более тяжелых случаях – жгучая боль в горле, чувство удушья, возможен отек гортани, легких, токсический бронхит , пневмония. При попадании концентрированных растворов в желудочно-кишечный тракт образуются глубокие некрозы, в острой стадии приводящие к болевому шоку. Массивные пищеводно-желудочные кровотечения, асфиксия в результате ожога и отека гортани, тяжелая ожоговая болезнь, реактивный перитонит. Смерть может наступить в первые часы и сутки от болевого шока, а в более поздние сроки – от ожоговой болезни и присоединившихся осложнений (массивное кровотечение, аспирационная пневмония, перфорация пищевода и желудка, медиастинит).

Первая медицинская помощь. Вывести пострадавшего из токсической среды; и промыть пораженные участки кожи и слизистых оболочек глаз большим количеством воды. Пить теплое молоко с боржоми или с содой. Режим молчания. При спазме голосовой щели и явлении отека гортани – горчичники и согревающий компресс на шею, горячие ножные ванны. Вдыхание паров лимонной или уксусной кислот, масляные ингаляции и ингаляции с антибиотиками. В глаза закапывать каждые два часа 30% раствор сульфацила натрия, 12% раствор новокаина или 0,5% раствор дикаина. В нос - сосудосуживающие средства (3% раствор эфедрина). Внутрь – кодеин (0,015 г), дионин (0,01 г). Внутривенно или подкожно – морфин, атропин, при удушье трахеотомия.

Рассмотрим утечку 75 тонн аммиака, произошедшую на трассе недалеко от исследуемого объекта. Скорость ветра 2 м/с, степень вертикальной устойчивости воздуха – инверсия. Проведем расчет размеров и площади зоны заражения, а также время подхода зараженного облака к зданию.

Глубину зоны заражения определим из таблицы “Глубина распостранения облаков зараженного воздуха с поражающими концентрациями АХОВ на открытой местности”. На открытой местности примасе аммиака в 75 тонн, при различных условиях она равна:

- при инверсии – Г=12 км;

- при изотермии – Г=2,4 км;

- при конвенции – Г= 0,48 км.

Поправочные коэффициенты для учета влияния скорости ветра на глубину распространения зараженного воздуха при скорости ветра 2 м/с:

- при инверсии – 0,6;

- при изотермии – 0,7;

- при конвенции – 0,7.

По условию задачи емкость обвалована, следовательно, глубина распространения зараженного воздуха Гр (км) вычисляется:

- при инверсии – Г=12*0,6/1=7,2 км;

- при изотермии – Г=2,4*0,7/1=3,429 км;

- при конвенции – Г= 0,48*0,7/1=0,686 км.

Ширина Ш, км, зоны химического заражения зависит от степени вертикальной устойчивости воздуха и определяется по формуле:

Ш=К*Г, где

Г – глубина распространения облака зараженного воздуха с поражающей концентрацией в км.

Степень вертикальной устойчивости воздуха (К) определяется по следующим соотношениям:

- при инверсии – К=0,03;

- при изотермии – К=0,15;

- при конвенции – К=0,3.

Получаем искомую ширину:

- при инверсии – Ш=0,03*7,2=0,216 км;

- при изотермии – Ш=0,15*3,429=0,514 км;

- при конвенции – Ш=0,3*0,686=0,206 км.

Площадь зоны заражения S, км2, определим по формуле:

S=0,5*Ш*Г

И составляет:

- при инверсии – S=0,778 км2;

- при изотермии – S=0,881 км2;

- при конвенции – S=0,141 км2.

Расчет времени при пожаре.

В помещении, где находится проектируемая система, из чрезвычайных ситуаций наиболее вероятной может оказаться возникновение пожара.

Основными параметрами, характеризующими процесс эвакуации из зданий и сооружений, являются:

- плотность людского потока (D);

- скорость движения людского потока (V);

- пропускная способность пути (Q);

- интенсивность движения (q);

- длина эвакуационных путей, как горизонтальных, так и наклонных (L);

- ширина эвакуационных путей (b);

Плотность людского потока, включающего N человек, рассчитаем по формуле:

Образование высоких плотностей наиболее вероятно и наиболее опасно в случае вынужденной эвакуации, когда люди стремятся быстрее уйти от источника опасности.

Время движения людского потока на любом этапе эвакуации определяется по формуле:

, где

V – скорость движения людского потока V на участке, которая определяется в зависимости от плотности людского потока D.

Скорость движения людского потока зависит от его плотности и вида пути (горизонтальные или наклонные). С увеличением плотности потока скорость движения уменьшается.

Расчетное время эвакуации людей Т определяется как сумма времени движения людского потока по отдельным участкам пути, рассчитываем по формуле:

Т=t1+t2+…+tn , где

T1, t2, …, tn – время движения потока людей на каждом этапе эвакуации.

При движении вниз по лестнице при небольшой плотности людского потока скорость выше, чем на горизонтальных участках, но при его возрастании люди перестают видеть ступени перед собой и скорость наоборот снижается.

Пропускной способностью пути называют количество людей, проходящих в единицу времени через поперечное сечение пути шириной b, рассчитываем по формуле:

Q=D*V*b

Интенсивностью движения людского потока называется величина, равная произведению плотности потока и скорости движения. Интенсивность движения не зависит от ширины пути, рассчитывается по формуле:

Q=D*V

Путь для эвакуации – проход по коридору налево к выходу и рассеивание по улице. Рассчитаем характеристику пути и введем результаты в табл. 5.7.

Таблица 5.7 – Характеристики пути эвакуации.

Путь	Всего человек	Длина пути (м)	Ширина пути (м)	Плотность (чел/м2)	Скорость (м/мин)	Время (мин)	Пропускная способность (чел/мин)	Интенсивность (чел/мин)
Коридор	30	7	4	1,07	37	0,19	158,57	39,64
Лестница	40	30	1,5	0,89	43	0,70	57,33	38,22

По таблице 5.7 и формуле определим время эвакуации людей:

Т=0,19+0,70=0,87 мин.≈53 с.

Из расчетов следует, что эвакуация из диспетчерской пройдет за короткое время, и в рамках поставленной задачи имеется довольно большой запас по времени, что является благоприятствующим фактором для проведения следующих этапов эвакуации персонала в безопасные зоны.

Вывод: в данном разделе дипломной работы были изложены требования к рабочему месту инженера – программиста. Созданные условия должны обеспечивать комфортную работу. На основании изученной литературы по данной проблеме, были указаны оптимальные размеры рабочего стола и кресла, рабочей поверхности, а также проведен выбор системы и расчет оптимального освещения производственного помещения, а также расчет уровня шума на рабочем месте. Соблюдение условий, определяющих оптимальную организацию рабочего места инженера, позволит сохранить хорошую работоспособность в течение всего рабочего дня, повысит как в количественном, так и в качественном отношениях производительность труда программиста, что в свою очередь будет способствовать повышению качества работы с аппаратурой.

Заключение

В результате проведенных исследований разработано программное средство воспроизведения зашумленного доплеровского сигнала, обеспечивающее: детерминированность параметров доплеровского колебания; воспроизведение полетного закона соотношения С/Ш; воспроизведение начального и конечного значений доплеровского колебания. Особенностью способа воспроизведения является использование в качестве модели шумовой помехи последовательность ПСП, которые близки при их воспроизведении по корреляционным характеристикам к параметрам белого шума. Разработанное программное средство воспроизведения зашумленного доплеровского сигнала адаптировано к типовым узлам ДИИС.

Список использованных источников

Артиллерия / Н.Н. Туркин, [и др.] ; под ред. М.Н. Чистякова. – М.: Воениздат МО СССР, 1953. – 478 с.
Архангельский, А.Я. Программирование в C++ Builder0 / А.Я. Архангельский. - М.: Бином, 2003. – 1151 с.
Бакулев, П.А. Радиолокационные системы / П.А. Бакулев. - М.: Радиотехника, 2004. – 320 с.
Баранов, Л.А. Квантование по уровню и временная дискретизация в цифровых системах управления / Л.А. Баранов – М.: Энергоатомиздат, 1990. – 304 с.
Бобнев, В.П. Генерирование случайных сигналов / В.П. Бобнев. – М.: Энергия, 1971. – 240 с.
Боков, А.С. Имитация радиолокационного сигнала, отраженного от движущейся цели / Боков А.С. [и др.] // Вестник УГТУ УПИ. - 2005. - №19. – С. 13 – 14.
Букингем, М. Шумы в электронных приборах и системах / М. Букингем. - М.: Мир, 1986. - 400с.
Гмурман, В.Е. Теория вероятностей и математическая статистика / В.Е. Гмурман. – М.: Высш. школа, 1977. – 479 с.
Гоноровский, И.С. Радиотехнические цепи и сигналы: учебник для вузов / И.С. Гоноровский. – М.: Сов. радио, – 672 с.
Давенпорт, В.Б. Введение в теорию случайных сигналов / В.Б. Давенпорт, В.Л. Рут ; пер. Б.Г. Белкина – М.: Изд. иностранной литературы, 1960. - 468с.
Кнут, Д.Э. Искусство программирования: уч. пособие. / Д.Э. Кнут. - М.: Издательский дом «Вильямс», 2000.- 832с.
Корн, Г. Справочник по математике / Г. Корн, Т. Корн ; под ред. И.Г. Арамановича. – М.: Наука, 1978. – 832 с.
Косарев, Н.А. Метод и средство воспроизведения зашумленных доплеровских сигналов / В.Н.Булатов, Н.А.Косарев, Е.С. Тимонов // Проблемы управления и моделирования в сложных системах: тр. XI международной конференции (22-24 июня 2009 г. Самара, Россия) ; Под ред. акад. Е.А.Федосова, акад. Н.А.Кузнецова, проф. В.А. Виттиха. – Самара: Самарский научный центр РАН, 2009. - С. 354-362.
Косарев, Н.А. Спектрально-временной метод обработки цифровых сигналов с неравномерной дискретизацией / В.Н.Булатов, Н.А.Косарев, Е.С. Тимонов // материалы VII всероссийской научно-техническая конференция «Информационные технологии в электротехнике и электроэнергетике». – Чебоксары: Изд. Чувашского ун-та. - 2010. - С. – 31 - 43.
Кук, Ч. Радиолокационные сигналы / Ч. Кук, М. Берифельд. – М.: Сов. Радио, 1971. – 568 с.
Радиотехнические схемы на транзисторах и туннельных диодах / И.И. Акулов [и др.]. - М.: Связь, 1966. – 512 с.
Разработка математических моделей зашумленных доплеровских колебаний: отчет о НИР (промежуточ.): Н. Тагильский ин-т испытания металлов ; рук. Булатов В.Н. ; исполн.: Косарев Н.А. [и др.]. – : ГОУ , 2008. – 31с. - Библиограф.: с. 29-30. - Инв. №2274.
Сергиенко, А.Б. Цифровая обработка сигналов / А.Б. Сергиенко. - СПБ.: Питер, 2002. – 808с.
Соловьев, А.Г. Тракт цифровой обработки сигналов когерентной импульсно-доплеровской РЛС / А.Г. Соловьев // Цифровая обработка сигналов. - 2000. - №2. – С. 5 – 6.
Тартаковский, Г.П. Динамика систем АРУ / Г.П. Тартаковский. – М.: Советское радио, – 191 с.
Финкельштейн, М.И. Основы радиолокации / М.И. Финкельштейн. – М.: Советское радио, 1973. – 492с.
Шнайер, Б. Прикладная криптография, Протоколы, алгоритмы, и исходные тексты на С++ / Б. Шнайер. - М.: Бином, 2005. – 354 с.
Янчук, Е.В. Туннельные диоды в приемо-усилительных устройствах / Е.В. Янчук. - М.: Энергия, 1967. - 55с.
Ярмолик, В.Н. Генерирование и применение псевдослучайных сигналов в системах испытаний и контроля / В.Н. Ярмолик, С.Н. Демиденко. - Минск: Наука и техника, 1986. – 200 с.
Сайт: Нижнетагильский институт испытания металлов : [Электронный ресурс]. – (http://www.ntiim.ru). – Проверено 02.12.2010.
Сайт: Радиолокация и радиометрия : [Электронный ресурс]. – (http://www. radio-location.org/). – Проверено 02.12.2010.
Viega, J. Secure Programming Cookbook for C and C++ / J. Viega, Z. Girouard, M. Messier. - London: Artech house inc, 2001. – 301 с.
Blum, L. A Simple Unpredictable Pseudo-Random Number Generator. / L. Blum, M. Blum, M. Shub. - SIAM, 1986. – 383 с.

Приложение А

(Справочное)

Раскладка программы для генерирования шума изображена на рисунке А.1.

Рисунок А.1 – Раскладка «Генератор шума»

Входные данные:

Способ генерирования ПСП:

Линейная конгруэнтная последовательность (рисунок А.1):

Множитель – значение параметра a;

Приращение – значение параметра с;

Начальное значение – значение параметра X₀;

Библиотечный модуль пакета С++;
Метод последовательности Фибоначчи с запаздыв. (рисунок А.2):

Начальные значения – значения массива ;

Запаздывания - значение параметров ;

Рисунок А.2

Метод регистра сдвига с обратными связями (рисунок А.3):

Начальные значения – значение параметра a₀;

Пропускать – значение параметра a_j;

Полином – многочлен ;

Рисунок А.3

5) Метод перемешивания (рисунок А.4);

Размер буфера – значение размера буфера;

Опция «Зациклить» – выполняет перемешивание n - раз;

Менять числа – изменяет числа при перемешивании;

Рисунок А.4

Интервал сохранения – при генерации ПСП в качестве последовательной выборки используется только каждый j-ый элемент генерируемой последовательности чисел;

Количество чисел – количество генерируемых чисел ПСП;

Для оценки качества ПСП используются пять статистических тестов, рекомендованных стандартом FIPS 140 национального института стандартов США. Для настройки критериев теста предназначено диалоговое окно (Настройки→Настройка критериев теста) изображенное на рисунке А.5.

Рисунок А.5

Опция «Стандарт FIPS 140-1» устанавливает значения критериев, рекомендованные стандартом FIPS 140.

Выходные данные:

В результате выполнения тестов выводится диалоговое окно с результатом «прошел/не прошел», и значениями критериев (рисунке А.6).

Рисунок А.6

Раскладка программы для задания параметров модели зашумленного доплеровского сигнала изображена на рисунке А.7.

Рисунок А.7 – Раскладка «Модель Доплеровского сигнала»

Входные данные:

Количество чисел – количество генерируемых чисел ПСП;

Частота дискретизации – значение параметра F, МГц;

Начальная частота - значение параметра ;

- значение параметра функции изменения частоты;

Время интегрирования – значение параметра ;

Эффективное значение – значение параметра ;

Отношение С/Ш в нач. – значение параметра ;

Отношение С/Ш в кон. – значение параметра ;

Опция «Включить АРУ» - нормировать сигнал;

Опция «Добавлять шум» смешивает сигнал со сгенерированным ранее шумом.

Выходные данные:

Общий вид результата можно увидеть на вкладке «Графики» после выполнения моделирования (рисунок А.8).

Рисунок А.8

В программе предусмотрена возможность сохранять (Файл®сохранить как…) модель доплеровского сигнала в двух форматах:

- в формате ASCII с приведенной погрешностью d_ASCII = 1/(2³¹- 2);

- в формате *.ADC (ADLink PCI 9812) (рисунок 11) с приведенной погрешностью d_A_DC= 1/(2ⁿ^-1-1), где n – число разрядов АЦП со знакопеременным входным напряжением сигнала.

Текст программы:

Dopler_Project.cpp;

#include <vcl.h>

#pragma hdrstop

USEFORM("Dopler.cpp", Form1);

USEFORM("Utest.cpp", Ftest);

USEFORM("Ugraph.cpp", Graph);

USEFORM("Uoption.cpp", Option);

USEFORM("Usave.cpp", Save);

WINAPI WinMain(HINSTANCE, HINSTANCE, LPSTR, int)

{

Application->Initialize();

Application->CreateForm(__classid(TForm1), &Form1);

Application->CreateForm(__classid(TGraph), &Graph);

Application->CreateForm(__classid(TFtest), &Ftest);

Application->CreateForm(__classid(TOption), &Option);

Application->CreateForm(__classid(TSave), &Save);

Application->Run();

}

Dopler.h;

…

#include <Graphics.hpp>

#include <Buttons.hpp>

#include <stdlib.h>

#include <math.h>

#include <Math.hpp>

class TForm1 : public TForm

{

__published: // IDE-managed Components

…

private: // User declarations

public: // User declarations

__fastcall TForm1(TComponent* Owner);

};

float dopfaza;

unsigned int *Data;

__int64 modul = 4294967297;

float *Signal;

bool res, longres = true;

unsigned int shift, amount;

const int smallRunLength[256] =

{

0, 1, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4, 4, 4, 4, 4,

5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5,

6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6,

7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7,

8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8,

8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8

};

//---------------------------------------------------------------------------

extern PACKAGE TForm1 *Form1;

//---------------------------------------------------------------------------

#endif

Dopler.cpp;

#include <vcl.h>

#pragma hdrstop

#include "Dopler.h"

#include "Utest.h"

#include "Ugraph.h"

#include "Uoption.h"

//---------------------------------------------------------------------------

#pragma package(smart_init)

#pragma resource "*.dfm"

TForm1 *Form1;

//---------------------------------------------------------------------------

__fastcall TForm1::TForm1(TComponent* Owner)

: TForm(Owner)

{

}

//ГЕНЕРАТОРЫ СЛУЧАЙНЫХ ЧИСЕЛ

//Метод линейной конгруэнтной последовательности

inline void linear_con(unsigned int amount, unsigned int shift)

{

unsigned __int64 a = _atoi64(Form1->Edit10->Text.c_str());

unsigned int c = StrToInt(Form1->Edit9->Text);

unsigned int Number0 = StrToInt(Form1->Edit11->Text);

unsigned __int64 buf;

unsigned int q;

unsigned int r;

free(Data);

Data = (unsigned int*) calloc(amount,sizeof(unsigned int));

for (unsigned int j=0; j<amount; j++)

{

for (unsigned int k=0; k<shift; k++)

{

buf = (__int64)a*Number0 + c;

q = buf >> 32;

r = buf & 4294967295;

Number0 = r - q;

if (r<q)

Number0 = Number0 + 1;

}

*(Data+j) = Number0;

}

//Метод библиотечной функции

inline void bibli_gen(unsigned int amount, unsigned int shift)

{

unsigned int Number0;

free(Data);

Data = (unsigned int*) calloc(amount, sizeof(unsigned int));

randomize();

for (unsigned int j=0; j<amount; j++)

{

for (unsigned int q=0; q<shift;q++)

Number0 = _lrand() + _lrand();

*(Data+j) = Number0;

}

// Метод последовательности Фибоначчи

inline bool fibonachi_gen(unsigned int amount, unsigned int shift)

{

unsigned short delay[24] = {24,55, 38,89, 37, 100, 30, 127, 83, 258, 107, 378, 273, 607, 1029, 2281, 576, 3217, 4187, 9689, 7083, 19937, 9739, 23209};

unsigned int fib[23610];

int j1 = delay[2*(Form1->ComboBox2->ItemIndex)];

int k = delay[2*(Form1->ComboBox2->ItemIndex) + 1];

unsigned int Number0;

if ((Form1->ComboBox1->ItemIndex==1)&&(Form1->RadioButton4->Enabled==false))

{

ShowMessage("Сгенерируйте исходную последовательность");

return false;

}

if (Form1->ComboBox1->ItemIndex==0)

linear_con(k, shift);

for (unsigned int i=0; i<k; i++)

fib[i+1] = *(Data+i);

free(Data);

Data = (unsigned int*) calloc(amount, sizeof(unsigned int));

for (unsigned int j=0; j<amount; j++)

{

for (unsigned int q=0; q<shift;q++)

{

fib[k] = ((__int64)fib[k] + fib[j1])&4294967295;

Number0 = fib[k];

j1 - -;

k - -;

if (j1==0)

j1 = delay[2*(Form1->ComboBox2->ItemIndex) + 1];

if (k==0)

k = delay[2*(Form1->ComboBox2->ItemIndex) + 1];

}

*(Data+j) = Number0;

}

// Метод перемешивания массива

inline void peremesh_gen (unsigned int amount, unsigned int bufer)

{

unsigned int buf1, buf0, k;

unsigned int buf = *(Data+bufer+1);

bool per = (Form1->CheckBox2->Checked);

ldiv_t Z;

Z=ldiv(amount, bufer);

randomize();

for (unsigned int j=0; j<Z.quot; j++)

{

for (unsigned int q=0; q<buffer; q++)

{

k = random(bufer);

buf1 = *(Data + j*buffer + k);

*(Data + j*buffer + k) = buf;

if (per)

{

buf0 = _lrotl(buf1,2);

buf1 = _lrotr(buf1,2);

buf1 = buf1 + buf0;

}

buf = buf + buf1;

}

for (unsigned int j=0; j<bufer; j++)

{

k = random(bufer);

buf1 = *(Data + ((Z.quot - 1)*buffer + Z.rem) + k);

*(Data + ((Z.quot - 1)*buffer + Z.rem) + k) = buf;

if (per)

{

buf0 = _lrotl(buf1,2);

buf1 = _lrotr(buf1,2);

buf1 = buf1 + buf0;

}

buf = buf + buf1;

}

//ТЕСТЫ НА СЛУЧАЙНОСТЬ ПОСЛЕДОВАТЕЛЬНОСТИ

inline int countBits(int x)

{

x = x - ((x >> 1) & 0x55555555);

x = (x & 0x33333333) + ((x >> 2) & 0x33333333);

x = (x + (x >> 4)) & 0x0F0F0F0F;

x = x + (x >> 8);

x = x + (x >> 16);

x = x & 0x3F;

return x;

}

inline int runLength( unsigned int x )

{

int length = 0; // Длина серии

unsigned int y;

// Приводим X к каноническому виду

x = (x ^ (x - 1)) >> 1;

y = x >> 16; if( y ) { length += 16; x = y; }

y = x >> 8; if( y ) { length += 8; x = y; }

return length + smallRunLength[x];

}

inline int expectedRunsNumber(

int length, // Длина серии

int sequenceLength //Длина последовательности

{

return (sequenceLength - length + 3) / (1 << (length + 2));

}

//Монобитный тест

inline double monobitTest(int address,int sequenceLength)

{

int n1 = 0, n0 = 0;

double X1;

for( int i = 0; i < sequenceLength; i++ )

n1 += countBits(*(Data + address + i));

n0 = INT_BITS * sequenceLength - n1;

X1 = ((double)n1 - n0)*((double)n1 - n0) / ((double)INT_BITS * sequenceLength);

return X1;

}

//Покер тест

inline double pokerTest( int address, int sequenceLength)

{

const int blockNum = 1 << POKER_BLOCK_LEN;

const unsigned int blockMask = blockNum - 1;

unsigned int x;

int blockCounter[blockNum] = {0};

double X2 = 0;

for( int i = 0; i < sequenceLength; i++ )

{

x=*(Data + address + i);

for( unsigned int j = 0; j < INT_BITS / POKER_BLOCK_LEN; j++ )

{

blockCounter[ x & blockMask ]++;

x = x >> POKER_BLOCK_LEN;

}

for( int i = 0; i < blockNum; i++ )

X2 += blockCounter[i] * blockCounter[i];

X2 = X2 * blockNum * POKER_BLOCK_LEN / (INT_BITS * sequenceLength)

- (double)(INT_BITS * sequenceLength) / POKER_BLOCK_LEN;

return X2;

}

//Серийный тест

inline double runsTest( int address,int sequenceLength )

{

unsigned int x, next;

unsigned int last_bit;

int length, delta;

int bitsLeft;

int blocksNum[INT_BITS] = {0};

int gapsNum[INT_BITS] = {0};

int expected;

double X4 = 0;

bool res;

int i;

bitsLeft = INT_BITS;

x = *(Data + address);

for( i = 1; i < sequenceLength; i++ )

{

if( x == 0 || x == ~(unsigned int)0 )

{

longres = false;

return X4;

}

next = *(Data+address+i);

last_bit = x >> (bitsLeft - 1);

if( x & 1 )

{

length = runLength( ~x );

blocksNum[length]++;

x = x >> length;

bitsLeft - = length;

}

while( true )

{

length = runLength( x );

if( length >= bitsLeft )

{

length = bitsLeft;

break;

}

gapsNum[length]++;

bitsLeft -= length;

x = ~(x >> length);

length = runLength( x );

if( length >= bitsLeft )

{

length = bitsLeft;

break;

}

blocksNum[length]++;

bitsLeft - = length;

x = ~(x >> length);

}

if( (next & 1) == last_bit )

{

if( last_bit )

{

delta = runLength( ~next );

blocksNum[length + delta]++;

}

else

{

delta = runLength( next );

gapsNum[length + delta]++;

}

if( length + delta >= (int)INT_BITS )

{

longres = false;

return X4;

}

next = next >> delta;

bitsLeft = INT_BITS - delta;

}

else

{

if( last_bit )

blocksNum[length]++;

else

gapsNum[length]++;

bitsLeft = INT_BITS;

}

x = next;

}

expected = expectedRunsNumber( 1, INT_BITS * sequenceLength);

for( i = 1; expected >= 5; i++ )

{

X4 += (((double)blocksNum[i] - expected) * ((double)blocksNum[i] - expected) + ((double) gapsNum[i] - expected) * ((double) gapsNum[i] - expected)) / expected;

expected = expectedRunsNumber( i+1, INT_BITS * sequenceLength);

}

return X4;

}

//Автокорреляционный тест

inline double autocorTest( int address, int sequenceLength)

{

unsigned int x, next, shifted;

int autoCor = 0;

double X5 = 0;

x=*(Data+address);

for( int i = 1; i < sequenceLength; i++ )

{

next =*(Data + address + i);

shifted = (next << (INT_BITS - AUTOCOR_SHIFT_SIZE))

| (x >> AUTOCOR_SHIFT_SIZE);

autoCor += countBits( x ^ shifted );

x = next;

}

X5 = (2.0 * autoCor - INT_BITS * sequenceLength + AUTOCOR_SHIFT_SIZE)

/ sqrt( INT_BITS * sequenceLength - AUTOCOR_SHIFT_SIZE );

X5 = fabs( X5 );

return X5;

}

//РЕЗУЛЬТАТ ТЕСТА

inline void ret(double X0[5],bool res)

{

Ftest->Label10->Caption = FloatToStrF(X0[0], 2, 3, 1);

Ftest->Label11->Caption = FloatToStrF(X0[1], 2, 3, 1);

Ftest->Label12->Caption = FloatToStrF(X0[3], 2, 3, 1);

Ftest->Label14->Caption = FloatToStrF(X0[4], 2, 3, 1);

Ftest->Label16->Caption = "Не пройден";

Ftest->Label16->Font->Color = clRed;

if (X0[0]<StrToFloat(Option->Edit1->Text))

{

Ftest->Label16->Caption = "Пройден";

Ftest->Label16->Font->Color = clWindowText;

}

Ftest->Label17->Caption = "Не пройден";

Ftest->Label17->Font->Color = clRed;

if (X0[1]< StrToFloat(Option->Edit2->Text))

{

Ftest->Label17->Caption = "Пройден";

Ftest->Label17->Font->Color = clWindowText;

}

Ftest->Label18->Caption = "Не пройден";

Ftest->Label18->Font->Color = clRed;

if (X0[3]< StrToFloat(Option->Edit3->Text))

{

Ftest->Label18->Caption = "Пройден";

Ftest->Label18->Font->Color = clWindowText;

}

Ftest->Label19->Caption = "Не пройден";

Ftest->Label19->Font->Color = clRed;

if (res)

{

Ftest->Label19->Caption = "Пройден";

Ftest->Label19->Font->Color = clWindowText;

}

Ftest->Label20->Caption = "Не пройден";

Ftest->Label20->Font->Color = clRed;

if (X0[4]< StrToFloat(Option->Edit4->Text))

{

Ftest->Label20->Caption = "Пройден";

Ftest->Label20->Font->Color = clWindowText;

}

//ТЕСТЫ

inline void Test(unsigned int amount)

{

int sequenceLength = 625;

double X1 = 0,X2 = 0,X4 = 0,X5 = 0,X0[5] = {0};

longres = true;

bool res = true;

ldiv_t Z1;

Z1=ldiv(amount, sequenceLength);

for(unsigned int j=0; j<Z1.quot; j++)

{

X1=monobitTest(j*sequenceLength, sequenceLength);

if (X1>=X0[0])

X0[0] = X1;

X2=pokerTest(j*sequenceLength, sequenceLength);

if (X2>=X0[1])

X0[1] = X2;

X4=runsTest(j*sequenceLength, sequenceLength);

if (X4>=X0[3])

X0[3] = X4;

if (longres==false)

res=false;

X5=autocorTest(j*sequenceLength, sequenceLength);

if (X5>=X0[4])

X0[4 ]= X5;

}

for(unsigned int j=0; j<Z1.quot; j++)

{

X1=monobitTest((Z1.quot - 1)*sequenceLength + Z1.rem, sequenceLength);

if (X1>=X0[0])

X0[0] = X1;

X2=pokerTest((Z1.quot - 1)*sequenceLength + Z1.rem , sequenceLength);

if (X2>=X0[1])

X0[1] = X2;

X4=runsTest((Z1.quot - 1)*sequenceLength + Z1.rem , sequenceLength);

if (X4>=X0[3])

X0[3] = X4;

if (longres==false)

res = false;

X5=autocorTest((Z1.quot - 1)*sequenceLength + Z1.rem , sequenceLength);

if (X5>=X0[4])

X0[4] = X5;

}

ret(X0, res);

}

//ГЕНЕРИРУЕМ ШУМ

void __fastcall TForm1::Button1Click(TObject *Sender)

{

amount = StrToInt(Edit13->Text);

shift = StrToInt(Edit12->Text);

//Линейная конгруэнтная последовательность

if (RadioButton1->Checked)

{

linear_con(amount, shift);

modul = 4294967296;

}

//Библиотечная функция

if (RadioButton5->Checked)

{

bibli_gen(amount, shift);

modul = 4294967296;

}

//Последовательность Фибоначчи

if (RadioButton2->Checked)

{

if(fibonachi_gen(amount, shift)==false)

return;

modul = 4294967296;

}

//Регистр сдвига

if (RadioButton3->Checked)

{

bibli_gen(amount, shift);

modul = 4294967296;

}

//Перемешиваем последовательность

if (RadioButton4->Checked)

{

peremesh_gen(amount, StrToInt(Edit18->Text));

if(CheckBox5->Checked)

{

for (int s=0;s<StrToInt(Edit19->Text)-1;s++)

peremesh_gen(amount, StrToInt(Edit18->Text));

}

//Тестируем последовательность

Test(amount);

RadioButton4->Enabled = true;

GroupBox1->Enabled = true;

N4->Enabled = true;

Option->RadioButton4->Enabled=true;

//Выводим результат

Ftest->ShowModal();

}

//МОДЕЛЬ ДОПЛЕРОВСКОГО СИГНАЛА

void __fastcall TForm1::Edit8Enter(TObject *Sender)

{

float aw = 2*M_PI*StrToFloat(Form1->Edit6->Text);

float bw = StrToFloat(Form1->Edit7->Text);

int N = StrToInt(Form1->Edit1->Text);

float Td = 1/(StrToFloat(Form1->Edit3->Text)*1000000);

float w0 = 2*M_PI*StrToFloat(Form1->Edit5->Text)*1000;

float w = 100*((aw/(1 + bw*N*Td))*N*Td)/w0;

Edit8->Text=FloatToStrF(w, 3, 3, 1);

}

//ГЕНЕРИРУЕМ СИГНАЛ

void __fastcall TForm1::Button2Click(TObject *Sender)

{

if ((StrToInt(Edit1->Text)>StrToInt(Edit13->Text))&&(CheckBox3->Checked==true))

{

ShowMessage("Количество выборок должно быть меньше "+Edit13->Text);

return;

}

float n1 = 2.4494*pow(10, StrToFloat(Form1->Edit4->Text)/20);

float n2 = 0.4082*pow(10, StrToFloat(Form1->Edit2->Text)/20);

float a = (n1*n2 - 1)/(StrToInt(Edit1->Text) - 1);

float Td = 1/(StrToFloat(Form1->Edit3->Text)*1000000);

float aw = StrToFloat(Form1->Edit6->Text);

float bw = StrToFloat(Form1->Edit7->Text);

unsigned int N = StrToInt(Form1->Edit1->Text);

float w0 = 1000*StrToFloat(Form1->Edit5->Text);

float buf;

unsigned int tau = StrToInt(Edit20->Text);

float eff = StrToFloat(Edit21->Text);

float bufer, usil, bufer1;

free(Signal);

Signal = (float*) calloc(N, sizeof(float));

Graph->Chart1->LeftAxis->Maximum = 1.1*StrToFloat(Form1->Edit5->Text);

Graph->Series2->Clear();

Graph->Series3->Clear();

for (unsigned int i=0; i<N; i++)

{

dopfaza = w0 - (aw/( 2 + 2*bw*i*Td))*i*Td;

if (CheckBox1->Checked)

Graph->Series3->AddXY(i*Td*1000,(w0-(aw/(1+1*bw*i*Td))*i*Td)*0.001,"",clRed);

//Сигнал без шума

*(Signal+i)=(cos(2*M_PI*dopfaza*i*Td))/(a*i+1-a);

//Сигнал с шумом

if (CheckBox3->Checked)

*(Signal+i)=(*(Signal+i))/2+((float)(*(Data+i)-modul/2))/(n1*modul);

}

for (unsigned int k=0;k<N-tau;k++)

{

if (CheckBox4->Checked)

{

bufer=0;

for (unsigned int i=k;i<k+tau;i++)

bufer=bufer+(*(Signal+i))*(*(Signal+i));

bufer1=bufer/tau;

usil=sqrt(eff/bufer1);

*(Signal+k)=(*(Signal+k))*usil;

}

if (*(Signal+k)>1)

*(Signal+k)=1;

if (*(Signal+k)<-1)

*(Signal+k)=-1;

if (CheckBox1->Checked)

Graph->Series2->AddXY(k*Td*1000,*(Signal+k),"",clRed);

}

N4->Enabled=true;

Option->RadioButton2->Enabled=true;

if (CheckBox1->Checked)

Graph->ShowModal();

}

//СОХРАНЯЕМ СИГНАЛ В ФОРМАТЕ ASCII

void file_ASCII()

{

unsigned int N;

int buf;

if(Option->RadioButton4->Checked)

N=StrToInt(Form1->Edit13->Text);

if(Option->RadioButton2->Checked)

N=StrToInt(Form1->Edit1->Text);

Form1->SaveDialog1->Execute();

ofstream outfile(Form1->SaveDialog1->FileName.c_str());

if (!outfile)

{

ShowMessage("Невозможно создать файл ASCII");

return;

}

for (int i=0;i<N;i++)

{

//Сохраняем Шум

if(Option->RadioButton4->Checked)

buf=(int)(*(Data+i)-modul/2);

//Сохраняем Модель сигнала

if(Option->RadioButton2->Checked)

buf=(int)((modul/2-2)*(*(Signal+i)));

outfile<<buf<<endl;

}

outfile.close();

}

//СОХРАНЯЕМ СИГНАЛ В ФОРМАТЕ ADC

void file_adc()

{

unsigned int N;

int bufer;

short buf;

if(Option->RadioButton4->Checked)

N=StrToInt(Form1->Edit13->Text);

if(Option->RadioButton2->Checked)

N=StrToInt(Form1->Edit1->Text);

Form1->SaveDialog2->Execute();

int handle;

if ((handle=open(Form1->SaveDialog2->FileName.c_str(),O_CREAT | O_WRONLY|O_BINARY))==-1)

{

ShowMessage("Невозможно создать файл");

return;

}

buf=1;

write(handle,&buf,2);

buf=(short)(40/StrToFloat(Form1->Edit3->Text));

write(handle,&buf,2);

for (unsigned int i=0;i<N;i++)

{

if(Option->RadioButton4->Checked)

buf=(((*(Data+i)-modul/2)>>16)&65535);

if(Option->RadioButton2->Checked)

{

bufer=(int)((modul/2-2)*(*(Signal+i)));

buf=((bufer>>16)&65535);

}

write(handle,&buf,2);

}

close(handle);

}

//СОХРАНЯЕМ

void __fastcall TForm1::N4Click(TObject *Sender)

{

if(Option->RadioButton1->Checked)

file_ASCII();

if(Option->RadioButton3->Checked)

file_adc();

}

ПРЕЗЕНТАЦИЯ К ДИПЛОМНОМУ ПРОЕКТУ

ЧЕРЧЕЖИ К ДИПЛОМНОМУ ПРОЕКТУ

Скачать дипломный проект: v-pechat.rar

Категория: Дипломные работы / Дипломные работы по электронике

Уважаемый посетитель, Вы зашли на сайт как незарегистрированный пользователь.
Мы рекомендуем Вам зарегистрироваться либо войти на сайт под своим именем.

Привет студент