Факультет экономики и управления
Кафедра математических методов и моделей в экономике
ОТЧЕТ
по индивидуальному заданию
по курсу «Случайные процессы и основы теории массового обслуживания»
на тему: «Аппроксимация спектральной плотности»
Постановка задачи
Дана ковариационная функция.
- Построить спектральную плотность;
- Восстановить формирующий фильтр по спектральной плотности;
- Записать ДУ и разностное уравнение, которое порождается белым шумом;
- Сгенерировать траекторию белого шума и получить случайный процесс.
1 Построение спектральной плотности для дискретного случайного процесса
Дана ковариационная функция: .
В дискретном случае мы применяем к ковариационной функции z-преобразование. В результате, получаем формулу для нахождения спектральной плотности:
После некоторого преобразования формула для определения спектральной плотности примет следующий вид:
где
Таким образом, ; .
То есть,
Вычислим отдельно .
Проинтегрируем данное выражение по переменной m.
Таким образом, ,
В результате,
После приведения к общему знаменателю, получим:
Из полученного выражения определяем коэффициенты разностного уравнения:
b0=;
Запишем полученное разностное уравнение:
.
Случайный процесс, порожденный белым шумом , имеет следующий вид:
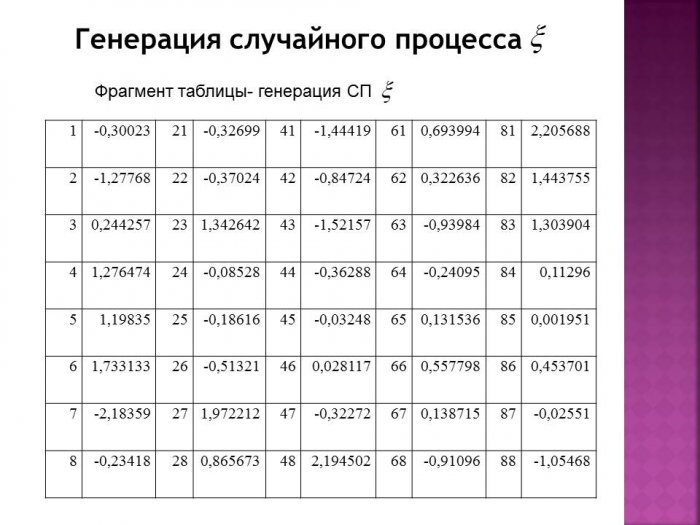
Сгенерируем случайный процесс ξ в МПП Excel (таблица 1).
Таблица 1- Генерация случайного процесса
|
1 |
-0,30023 |
21 |
-0,32699 |
41 |
-1,44419 |
61 |
0,693994 |
81 |
2,205688 |
|
2 |
-1,27768 |
22 |
-0,37024 |
42 |
-0,84724 |
62 |
0,322636 |
82 |
1,443755 |
|
3 |
0,244257 |
23 |
1,342642 |
43 |
-1,52157 |
63 |
-0,93984 |
83 |
1,303904 |
|
4 |
1,276474 |
24 |
-0,08528 |
44 |
-0,36288 |
64 |
-0,24095 |
84 |
0,11296 |
|
5 |
1,19835 |
25 |
-0,18616 |
45 |
-0,03248 |
65 |
0,131536 |
85 |
0,001951 |
|
6 |
1,733133 |
26 |
-0,51321 |
46 |
0,028117 |
66 |
0,557798 |
86 |
0,453701 |
|
7 |
-2,18359 |
27 |
1,972212 |
47 |
-0,32272 |
67 |
0,138715 |
87 |
-0,02551 |
|
8 |
-0,23418 |
28 |
0,865673 |
48 |
2,194502 |
68 |
-0,91096 |
88 |
-1,05468 |
|
9 |
1,095023 |
29 |
2,375655 |
49 |
-1,74248 |
69 |
1,884846 |
89 |
-1,77481 |
|
10 |
-1,0867 |
30 |
-0,65491 |
50 |
-0,73648 |
70 |
0,487198 |
90 |
0,828331 |
|
11 |
-0,6902 |
31 |
1,661456 |
51 |
-2,57758 |
71 |
0,072239 |
91 |
0,444224 |
|
12 |
-1,69043 |
32 |
-1,6124 |
52 |
1,44767 |
72 |
0,829841 |
92 |
0,617906 |
|
13 |
-1,84691 |
33 |
0,538948 |
53 |
-1,27976 |
73 |
0,862008 |
93 |
0,213473 |
|
14 |
-0,97763 |
34 |
0,902191 |
54 |
-0,65358 |
74 |
-0,63653 |
94 |
-1,02693 |
|
15 |
-0,77351 |
35 |
1,918916 |
55 |
0,757714 |
75 |
-0,92319 |
95 |
1,238195 |
|
16 |
-2,11793 |
36 |
-0,08452 |
56 |
0,466712 |
76 |
1,111189 |
96 |
-0,31121 |
|
17 |
-0,56792 |
37 |
-0,5238 |
57 |
0,874609 |
77 |
-1,20118 |
97 |
-0,83992 |
|
18 |
-0,40405 |
38 |
0,675138 |
58 |
0,595742 |
78 |
-1,55889 |
98 |
-0,82113 |
|
19 |
0,134853 |
39 |
-0,38132 |
59 |
-1,37185 |
79 |
0,711325 |
99 |
-0,42899 |
|
20 |
-0,36549 |
40 |
0,757611 |
60 |
-1,11574 |
80 |
0,638406 |
100 |
-0,45336 |
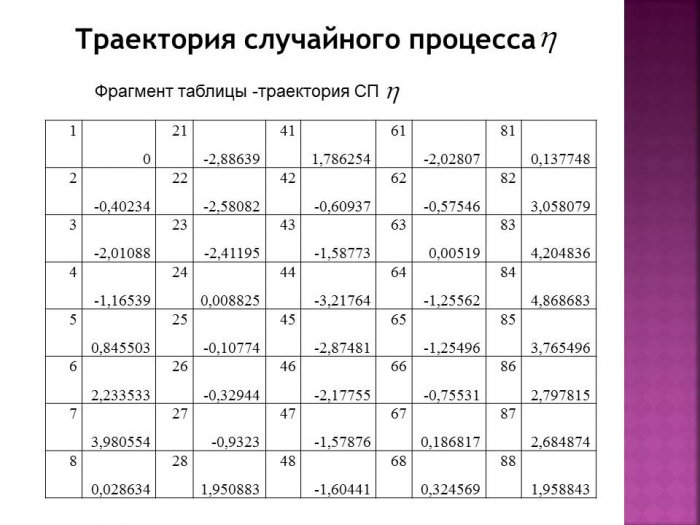
В результате, получим траекторию случайного процесса , порожденного белым шумом и с начальным условием (таблица 2).
Таблица 2- Траектория случайного процесса
|
1 |
0 |
21 |
-2,88639 |
41 |
1,786254 |
61 |
-2,02807 |
81 |
0,137748 |
|
2 |
-0,40234 |
22 |
-2,58082 |
42 |
-0,60937 |
62 |
-0,57546 |
82 |
3,058079 |
|
3 |
-2,01088 |
23 |
-2,41195 |
43 |
-1,58773 |
63 |
0,00519 |
83 |
4,204836 |
|
4 |
-1,16539 |
24 |
0,008825 |
44 |
-3,21764 |
64 |
-1,25562 |
84 |
4,868683 |
|
5 |
0,845503 |
25 |
-0,10774 |
45 |
-2,87481 |
65 |
-1,25496 |
85 |
3,765496 |
|
6 |
2,233533 |
26 |
-0,32944 |
46 |
-2,17755 |
66 |
-0,75531 |
86 |
2,797815 |
|
7 |
3,980554 |
27 |
-0,9323 |
47 |
-1,57876 |
67 |
0,186817 |
87 |
2,684874 |
|
8 |
0,028634 |
28 |
1,950883 |
48 |
-1,60441 |
68 |
0,324569 |
88 |
1,958843 |
|
9 |
-0,29257 |
29 |
2,60826 |
49 |
1,749847 |
69 |
-0,97984 |
89 |
0,040725 |
|
10 |
1,250251 |
30 |
5,119758 |
50 |
-1,03614 |
70 |
1,798514 |
90 |
-2,34817 |
|
11 |
-0,52819 |
31 |
2,922861 |
51 |
-1,7561 |
71 |
1,987963 |
91 |
-0,63305 |
|
12 |
-1,31703 |
32 |
4,396201 |
52 |
-4,75778 |
72 |
1,57251 |
92 |
0,125373 |
|
13 |
-3,24299 |
33 |
1,102624 |
53 |
-1,59178 |
73 |
2,279369 |
93 |
0,921118 |
|
14 |
-4,88236 |
34 |
1,54074 |
54 |
-2,89661 |
74 |
2,84719 |
94 |
0,969838 |
|
15 |
-4,93439 |
35 |
2,352741 |
55 |
-3,02607 |
75 |
1,260513 |
95 |
-0,65625 |
|
16 |
-4,69946 |
36 |
4,318009 |
56 |
-1,2309 |
76 |
-0,30146 |
96 |
1,172147 |
|
17 |
-6,32673 |
37 |
3,092082 |
57 |
-0,28829 |
77 |
1,265317 |
97 |
0,453053 |
|
18 |
-5,45752 |
38 |
1,593379 |
58 |
0,958055 |
78 |
-0,67042 |
98 |
-0,78926 |
|
19 |
-4,59269 |
39 |
2,087544 |
59 |
1,509532 |
79 |
-2,58673 |
99 |
-1,68627 |
|
20 |
-3,22853 |
40 |
1,038615 |
60 |
-0,71785 |
80 |
-0,96694 |
100 |
-1,82664 |
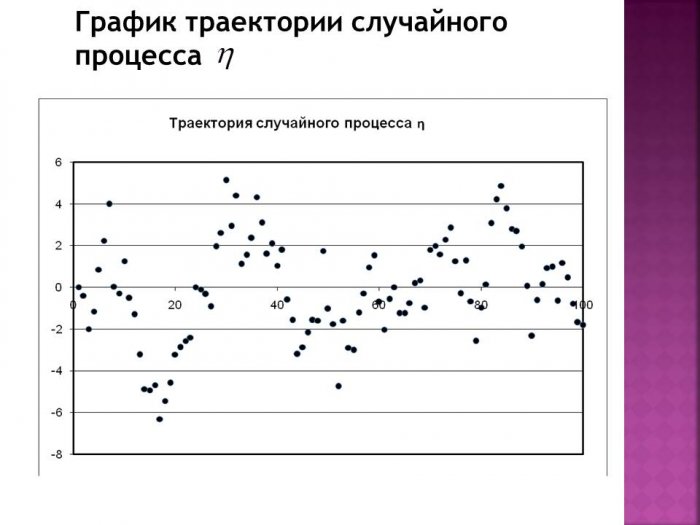
Полученная траектория случайного процесса представлена на рисунке 1.
Рисунок 1- график траетории случайного процесса
Вторая часть индивидуальной работы заключается в аппроксимации спектральной плотности для непрерывного случая.
2 Аппроксимация функций ортогональными рядами
Рассмотрим возможность аппроксимации функции произвольного вида ортогональными полиномами. Дана функция вида , определенная на интервале . Она может быть разложена в абсолютно сходящийся ряд вида:
, (2.1)
где – коэффициенты Фурье, – семейство базисных функций, ортонормированных на определенном интервале с весом .
Это семейство характеризуется интегралом:
(2.2)
– интервал, на котором выполняется условие ортонормированности указанных функций.
Следует подчеркнуть, что на практике приходится ограничиваться конечным числом ряда (2.1). Это приводит к появлению методической погрешности, значение которой зависит в немалой степени от способа оценки параметров модели.
Поэтому для модели аппроксимирующей функции
, (2.3)
имеющей ограниченное число параметров, коэффициенты разложения, обеспечивающие минимум среднеквадратической погрешности аппроксимации:
, (2.4)
определяются формулой:
. (2.5)
Выражение (2.5) получается из (2.4) при условии :
. (2.6)
Представим интеграл (2.6) в виде суммы интегралов и разнесем сумму в разные части равенства:
. (2.7)
С учетом (2.2) от выражения (2.7) мы переходим к выражению определения коэффициентов (2.5). При таком способе определения коэффициентов разложения погрешность аппроксимации, с учетом свойств ортогональных полиномов, равна:
.
3 Аппроксимация спектральной плотности
Спектральные функции представляют собой частотное распределение характеристик случайного процесса. Существуют различные способы их определения: преобразование Фурье процесса, преобразование Фурье ковариационной функции. Определим спектральную плотность мощности в виде:
. (3.1)
Можно установить связь между ковариационной функцией и спектральной плотностью:
(3.2)
С учетом четности функций и , воспользовавшись формулой Эйлера, выражения (3.1) и (3.2) приведем к виду:
; (3.3)
(3.4)
Аналитические выражения спектральной плотности для типовых моделей ковариационных функций приведены в таблице 3.
Таблица 3- Спектральные плотности
- Аппроксимация спектральной плотности ортогональными функциями
Определив параметры модели ковариационной функции b0,…,bm, α
(3.5)
оценим спектральную плотность случайного процесса.
Для этого, подставив модель (3.5) в выражения для определения спектральной плотности (3.1), получим:
. (3.6)
С учетом определения частотной характеристики ортогональных функций, получим:
(3.7)
Подставив в выражение (3.7) значения частотных характеристик, определим спектральную плотность для различных ортогональных базисов.
Ортогональный базис Лагерра
Подставив в выражение (3.7) значение частотной характеристики ортогонального базиса Лагерра, получим:
(3.8)
Введем обозначение
(3.9)
или
(3.10)
Воспользовавшись формулами Эйлера, выражение (3.10) приведем к виду:
=
=
где
коэффициент разложения ортогонального ряда;
- параметры ковариационной функции;
- значение взаимной корреляционной функции в точке максимума.
- Практическая часть
Известна ковариационная функция непрерывного случайного процесса:
.
Для восстановления спектральной плотности воспользуемся учебной программой «Аппроксимативный корреляционно-спектральный анализ».
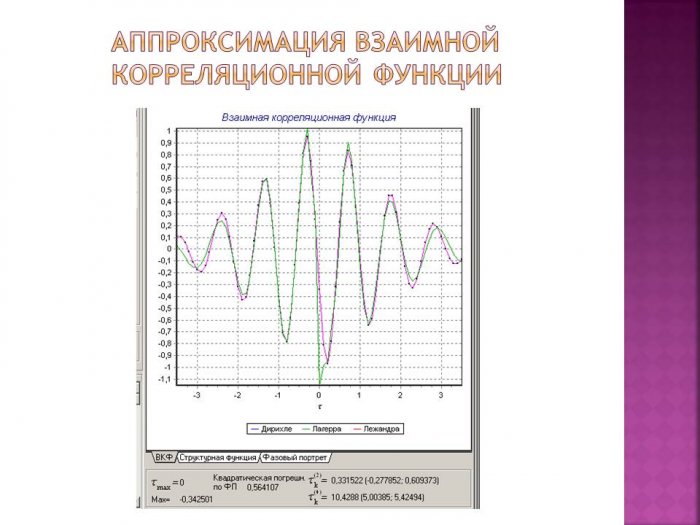
На рисунке 2 представлена аппроксимация взаимной корреляционной функции с помощью системы ортогональных функций Лагерра.
Рисунок 2- Аппроксимация ВКФ
На рисунке видим, что значение взаимной корреляционной функции в точке максимума =-0,343.
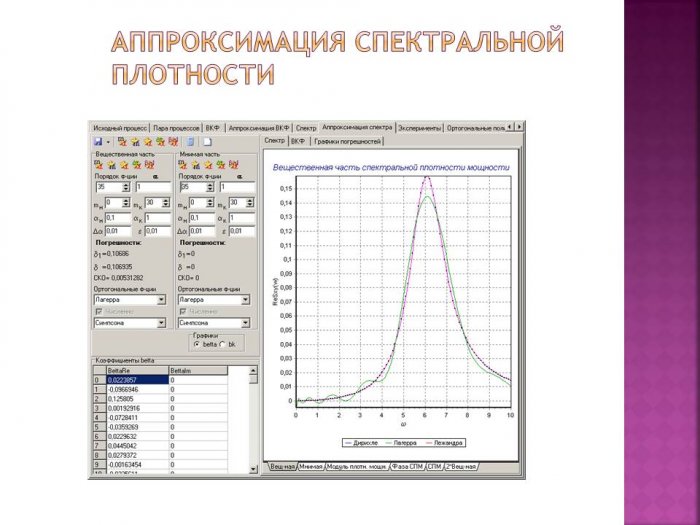
Аппроксимация спектральной плотности с помощью ортогональной функции Лагерра представлена на рисунке 3.
Рисунок 3- Аппроксимация спектральной плотности
Таким образом, параметры функции имеют следующий вид: =1; =6;
Порядок функции задаем таким образом, чтобы наиболее удачно аппроксимировать спектральную плотность ортогональными функциями Лагерра. Коэффициенты разложения представлены соответственно на рисунке 4: их количество равно порядку функции, то есть 9.
Рисунок 4- Коэффициенты разложения
Таким образом,
Спектральная функция, аппроксимируемая с помощью системы ортогональных функций Лагерра, имеет вид:
Учитывая ранее полученные данные, выражение для спектральной плотности запишется в виде:
В результате преобразований получен следующий результат:
Таким образом, коэффициенты дифференциального уравнения имеют следующий вид:
Случайный процесс, порожденный белым шумом , имеет следующий вид:
Таким образом, задавая конкретные значения параметра , можем сгенерировать траекторию белого шума и получить случайный процесс.
ПРЕЗЕНТАЦИЯ
Скачать: