Задача синтеза заключается в созданий системы регулирования по заданным переходным процессам. В инженерной практике из-за своей сложности и неопределенности она решается частично. Считается, что некоторая часть системы (объект и исполнительный орган) задана. В большинстве случаев задача синтеза системы регулирования сводится к подбору типа регулятора для известного объекта.
Задачей анализа является определение переходных процессов в полностью заданной системе регулирования. Работа системы регулирования должна быть устойчивой и удовлетворять основным требованиям к качеству процесса регулирования. Исходя из указанных условий, определяют настройку регулятора, которая во многом зависит от характеристик объекта. В связи с изменениями режимов работы холодильной установки нередко возникает необходимость изменения настройки регуляторов в условиях эксплуатации. Поэтому остановимся подробнее на инженерных методах анализа систем регулирования.
Устойчивость системы заключается в способности ее вернуться в состояние равновесия после того, как внешние силы вывели систему из этого состояния. Устойчивой работе системы соответствует затухающий характер процесса регулирования. В неустойчивой системе возникшая по каким-либо причинам погрешность регулирования с течением времени возрастает. Поскольку устойчивость автоматической системы является одним из основных ее показателей, необходима математическая формулировка условий устойчивости.
Переходный процесс в любой динамической системе можно разделить на две составляющие: а) свободное движение, определяемое начальными условиями и свойствами системы; б) вынужденное движение, определяемое внешним воздействием. Чтобы система была устойчивой, свободная составляющая переходного процесса с течением времени должна стремиться к нулю.
Динамика системы регулирования описывается системой дифференциальных уравнений, которую в линейном приближении можно свести к виду
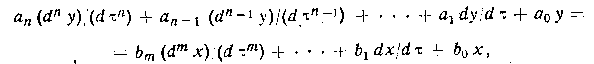
где х, у — входное воздействие и регулируемый параметр; аi, bi — постоянные коэффициtнты, определяемые параметрами системы; n, m — любые целые числа, причем m<n.
Свободное движение линейной системы описывается однородным дифференциальным уравнением, т. е. уравнением без правой части. После преобразования по Лапласу при нулевых начальных условиях из него получается характеристическое уравнение
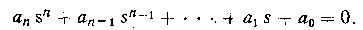
Корни характеристического уравнения si могут быть вещественными ai и комплексно-сопряженными (ак ± jвк). С учетом типа их решение однородного дифференциального уравнения записывается в виде
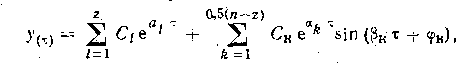
где Ci; Ск — постоянные интегрирования; z — число вещественных корней; фк — фазовый сдвиг.
Как видим, правая часть полученного решения стремится к нулю при условии аi<0 и ак<0. Следовательно, для устойчивости линейной системы регулирования необходимо и достаточно, чтобы все вещественные корни характеристического уравнения системы и вещественные части всех его комплексных корней были отрицательными. Если хотя бы один корень характеристического уравнения имеет положительную вещественную часть, то система регулирования неустойчива, так как регулируемый параметр при свободном движении системы неограниченно возрастает. При наличии нулевого корня система находится на границе устойчивости.
Таким образом, прямой путь определения устойчивости системы состоит в отыскании корней характеристического уравнения. При степени характеристического уравнения выше трех этот путь оказывается весьма трудоемким. Поскольку для суждения об устойчивости системы достаточно знать лишь знаки всех корней характеристического уравнения, из коэффициентов его составляют оценки, называемые критериями устойчивости. Простейшим необходимым (но недостаточным) критерием устойчивости является требование, чтобы все коэффициенты характеристического уравнения были одного знака, например положительными. Все предложенные критерии можно разделить на алгебраические и частотные.
Первый критерий устойчивости для системы третьего порядка в удобной для практики форме был предложен в 1876 г. И. А. Вышнеградским. Более общим критерием, пригодным для оценки устойчивости систем любого порядка, является критерий Рауса—Гурвица. Рассмотрим его в формулировке Гурвица.
Если характеристическое уравнение системы имеет вид, то для устойчивости линейной системы регулирования необходимо и достаточно, чтобы определитель Гурвица и все его диагональные миноры были положительными. Определитель n-го порядка составляется по следующему правилу; по диагонали располагаются коэффициенты, начиная с аn-1 до а0. Заполнение определителя идет по столбцам. Выше диагональных коэффициентов ставятся коэффициенты с убывающими индексами до aо. Остальные места выше заполняются нулями. Ниже диагональных коэффициентов ставятся коэффициенты с возрастающими индексами до аn. Остальные места выше заполняются нулями. Диагональные миноры получаются вычеркиванием справа и снизу последовательно по одной строке и одному столбцу, по две строки и два столбца и т. д. Для систем более высокого порядка можно пользоваться алгебраическим критерием Рауса—Гурвица, записанным в других формах. Соответствующий выбор формы записи критерия способствует уменьшению объема вычислительной работы.
Частотные критерии позволяют судить об устойчивости системы по виду построенной на комплексной плоскости кривой. Они обладают большой наглядностью и могут применяться к исследованию систем высокого порядка. В зависимости от исходных данных для построения кривой различают критерий Найквиста и критерий Михайлова.
Критерий Найквиста позволяет по виду амплитудно-фазовой характеристики (АФХ) разомкнутой системы определять устойчивость соответствующей замкнутой системы. АФХ разомкнутой системы может быть получена как аналитически, так и экспериментально, что выгодно отличает критерий Найквиста от других критериев. Формулируется он следующим образом. Если разомкнутая система устойчива или нейтральна, то для устойчивости замкнутой системы регулирования необходимо и достаточно, чтобы АФХ разомкнутой системы при изменении частоты от 0 до ос не охватывала точку с координатами (—1; iц). В противном случае замкнутая система неустойчива (пунктирная кривая). Если АФХ разомкнутой системы проходит через точку (—1; i0), то система в замкнутом состоянии находится на границе устойчивости. В такой системе возникают незатухающие колебания с частотой wп, при которой АФХ разомкнутой системы проходит через указанную точку.
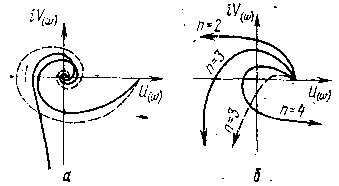
Рис. 1. Определение устойчивости системы регулирования:
а — по. критерию Найквиста; б — по критерию Михайлова
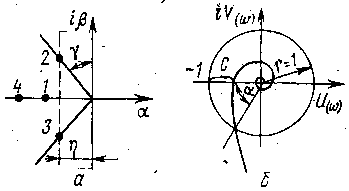
Рис. 2. Определение запаса устойчивости:
а — по расположению корней характеристического уравнения; б — по АФХ разомкнутой системы
Критерий Михайлова основан на рассмотрении кривой, получаемой из характеристического уравнения замкнутой системы. Для построения кривой Михайлова в характеристическом уравнении оператор Лапйаса s приравнивается к его мнимой части iw). В результате получается функция комплексного переменного:
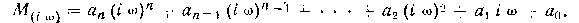
При изменении частоты со от 0 до оо вектор М(iw) на комплексной плоскости будет поворачиваться против часовой стрелки (т. е. в положительном направлении) около начала координат, изменяя одновременно и свою длину. Конец вектора на комплексной плоскости описывает кривую, называемую годографом.
Линейная система регулирования будет устойчива, если годограф вектора Михайлова при изменении частоты от 0 до оо обходит последовательно в положительном направлении, нигде не обращаясь в нуль, n квадратов, где n — степень характеристического уравнения системы. Если годограф вектора Михайлова проходит через 0, не заходя в очередной квадрант, то система на частоте, соответствующей прохождению вектора через 0, находится на границе устойчивости. При отклонениях от указанного выше поведения вектора система неустойчива.
Для нормальной работы система регулирования не только должна быть устойчивой, но и обладать определенным запасом устойчивости. О запасе устойчивости судят по отдаленности точки с параметрами реальной системы от границы устойчивости.
Запас устойчивости можно определить по расположению корней характеристического уравнения системы на комплексной плоскости. Для устойчивой системы все корни должны находиться в левой части этой плоскости. Удаленность корней от мнимой оси определяет зanac устойчивости системы.Расстояние n отражает удаленность ближайшей пары комплексных сопряженных корней от мнимой оси. Величина n характеризует степень устойчивости системы. Чаще запас устойчивости системы характеризуют углом у, составленным мнимой осью с лучом, соединяющим ближайший комплексный корень с началом координат.
Если свойства системы заданы ее частотными характеристиками, то запас устойчивости удобно определять по удаленности АФХ разомкнутой системы от точки с координатами (—1, i0). Он может быть выражен двумя величинами: запасом устойчивости по модулю С и запасом устойчивости по фазе а.
Качество процесса регулирования должно удовлетворять определенным требованиям. В частности, процесс регулирования должен затухать интенсивно. Система регулирования должна обеспечивать заданную статическую и динамическую точность. Время регулирования должно быть минимальным. В инженерной практике применяют прямые и косвенные. методы анализа качества процесса регулирования.
Прямые методы анализа предполагают непосредственное решение дифференциальных уравнений системы любым способом. Они являются наиболее точными, но, как правило, и наиболее трудоемкими. Применение их рационально для анализа систем невысокого порядка. Косвенные методы анализа позволяют оценивать качество процесса регулирования, не решая уравнений динамики. К ним относятся корневые методы, интегральные оценки и частотные методы.
Среди корневых методов наиболее простой и распространенной является оценка переходного процесса по степени устойчивости n, определяемой расстоянием на комплексной плоскости от мнимой оси до ближайшего к ней корня. Степень устойчивости называется апериодической, если ближайший к мнимой оси корень вещественный. Она называется колебательной, если ближайший к мнимой оси корень комплексный. В обоих случаях на переходный процесс доминирующее влияние оказывает экспонента, характеризуемая минимальным корнем.
Важным является то, что степень устойчивости можно определить без нахождения корней характеристического уравнения. Для этого в характеристическом уравнении переходят к новой переменной z = s + n. После подстановки s = z — n получается так называемое смещенное уравнение
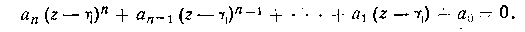
Его можно привести к виду
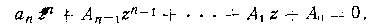
Выполненная замена переменной соответствует смещению осей на плоскости корней влево на величину n. В итоге один или два корня попадают на мнимую ось, что соответствует границе устойчивости. К смещенному характеристическому уравнению можно применить любой критерий устойчивости и найти, при каком значении n система оказывается на границе устойчивости.
Исследование качества процесса регулирования при помощи интегральных оценок сводится к нахождению определенных интегралов в пределах 0÷оо от некоторых функций отклонения регулируемого параметра. В инженерной практике используются условные интегральные показатели, которые удается вычислить, не решая дифференциального уравнения системы.
Используемая литература: Ейдвюс А. И. Системы и средства автоматизации судовых
холодильных установок. М.: Легкая и пищевая пром-сть,
1983.— с.
Скачать реферат:
Пароль на архив: privetstudent.com